Предмет: Алгебра,
автор: ignatevpavel05
Докажите, что число является рациональным.
Приложения:
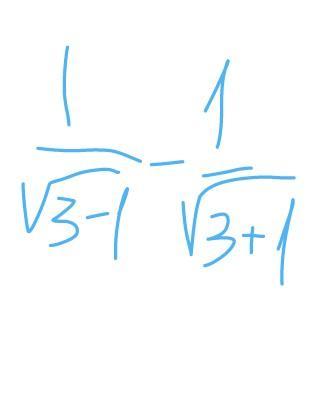
Кот49:
А тот, кто писал это задание, не мог ошибиться? У меня есть стойкое чувство, что это иррациональное число.
Не знаю
Как написано так и написал
Ну в любом случае доказать я это не могу. Но у препода лучше спроси, не ошибся ли он, если решения так и не будет.
Ответы
Автор ответа:
1
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: dimidrol1258
Предмет: Математика,
автор: krkatyark
Предмет: Русский язык,
автор: sadykidiev
Предмет: История,
автор: EduardPozzi
Предмет: Русский язык,
автор: plzhelp11111