Предмет: Алгебра,
автор: ShoyHinata
Помогите , даю 30 баллов.
Приложения:
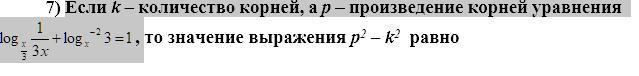
Ответы
Автор ответа:
1
Ответ:
5
Объяснение:
Область определения отсекает первый корень, т.е. решения всего два и
Похожие вопросы
Предмет: Математика,
автор: otarasova741
Предмет: Математика,
автор: 1656056
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: karinasha1
Предмет: Геометрия,
автор: Данил1вшуш