Question

помогите пожалуйста ​

Answer 1

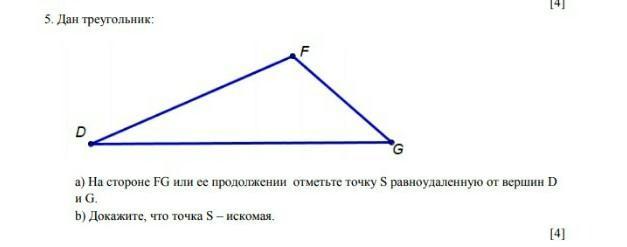
Дано ∆DFG.

Построить точку S

на прямой DG, такую, что SD = SG.

Решение:

Множ-во точек, равноудаленных от D и G - образуют срединный перпеедикуляр к отрезку DG.

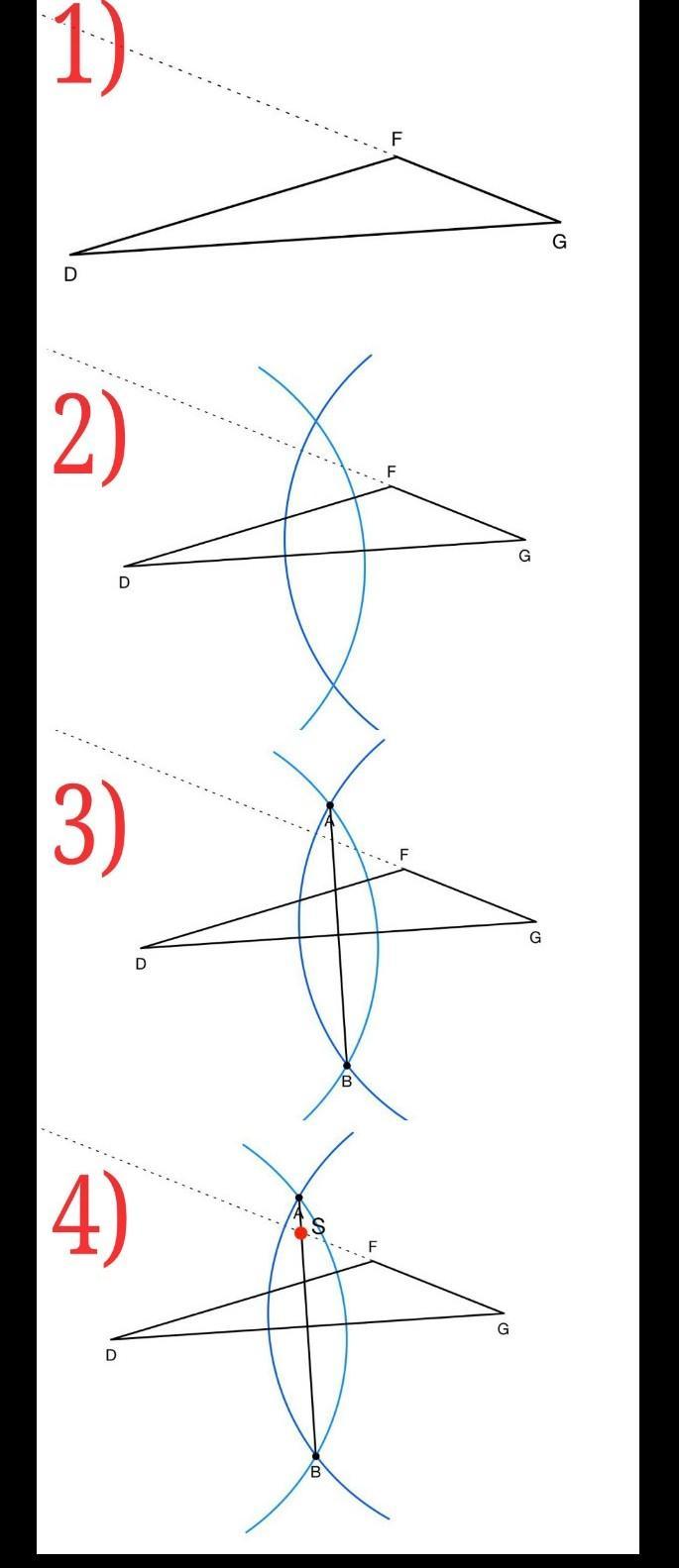
1) Построить луч продолжения отрезка GF

2) Построить срединный перпендикуляр можно по двум точкам пересечения окружностей равных радиусов и центрами в т.D и т.G. (R должен быть больше ½DG)

Пусть,окр. (D;R) пересек. окр. (G;R) = {А; В}

Тогда прямая АВ - будет срединным перпеедикуляром к DG.

3) Обозначить точку где АВ пересек. GF = S

4) S \in AB;\: S \in DG

$S \in AB;\: S \in DG = > S - uck. \: m.$