Предмет: Алгебра,
автор: serbenevaarina527
Решите неравенство пожалуйста ❤
Приложения:
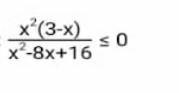
Ответы
Автор ответа:
1
Знаменатель свернем в (x-4)^2
x не может равен 4 по ОДЗ, значит (x-4)^2 > 0 и не влияет на знак дроби
Отсюда x^2 (3 - x) <= 0. Если x^2 = 0, то дробь тоже равна 0 и нас это устраивает, то есть x = 0 - один из корней. Теперь, аналогично знаменателю, x^2 > 0 и не влияет на знак, то есть 3 - x <= 0, отсюда x >= 3.
Ответ: {0} u [3 ; 4) u (4 ; + ∞ )
Автор ответа:
1
+ + - -
______[0]______[3]______(4)______
//////////////// ////////////
Похожие вопросы
Предмет: Русский язык,
автор: лерок33
Предмет: История,
автор: SashkaOmlet
Предмет: Русский язык,
автор: kairat20051
Предмет: Математика,
автор: asiaprian
Предмет: Английский язык,
автор: Jenyastai