Предмет: Геометрия,
автор: Аноним
((помогите пожалуйста)) Рисунок обязателен, 50 баллов, 1 задание!
Приложения:

Ответы
Автор ответа:
1
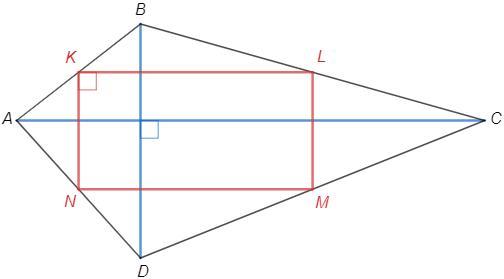
K, L, M, N - середины сторон произвольного четырехугольника ABCD
KL - средняя линия в треугольнике ABC => KL||AC, KL=AC/2
NM - средняя линия в треугольнике ADC => NM||AC, NM=AC/2
=> KL||NM, KL=NM
KLMN - параллелограмм (по признаку: две противоположные стороны параллельны и равны)
Доказали теорему Вариньона: середины сторон произвольного четырехугольника являются вершинами параллелограмма.
а) Диагонали ABCD перпендикулярны, следовательно стороны KLMN также перпендикулярны.
AC⊥BD, KL||AC, KN||BD => KL⊥KN
Параллелограмм с прямым углом - прямоугольник.
б) KL =AC/2; KN =BD/2
P(KLMN) =2(KL+KN) =AC+BD =10+5 =15 (см)
S(KLMN) =KL*KN =1/4 AC*BD =10*5/4 =12,5 (см^2)
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: Mika797
Предмет: Математика,
автор: ДаркаМалка
Предмет: Литература,
автор: daryakolomoets
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: давід5
- стороны параллельны диагоналям ч-ка и равны их половинам
- углы равны углам между диагоналями ч-ка
- периметр равен сумме диагоналей ч-ка
- площадь равна 1/2 площади ч-ка