Предмет: Алгебра,
автор: ns110376s
решите систему уравнений
Приложения:
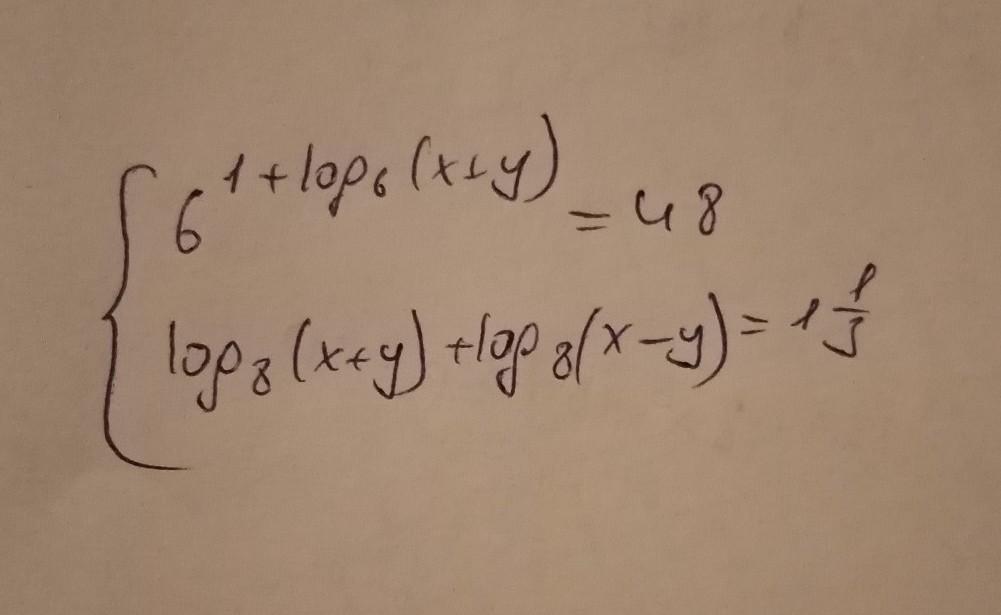
Ответы
Автор ответа:
1
Ответ:
Приложения:
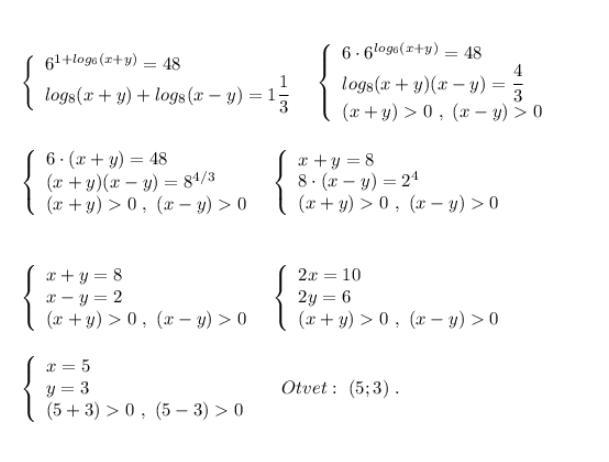
Похожие вопросы
Предмет: Английский язык,
автор: maryam7
Предмет: Русский язык,
автор: Аида4G
Предмет: Окружающий мир,
автор: Анэрика
Предмет: Информатика,
автор: 201075
Предмет: Алгебра,
автор: artemegoyan200p6pn00