Предмет: Алгебра,
автор: ns110376s
решите неравенство решите неравенство
Приложения:
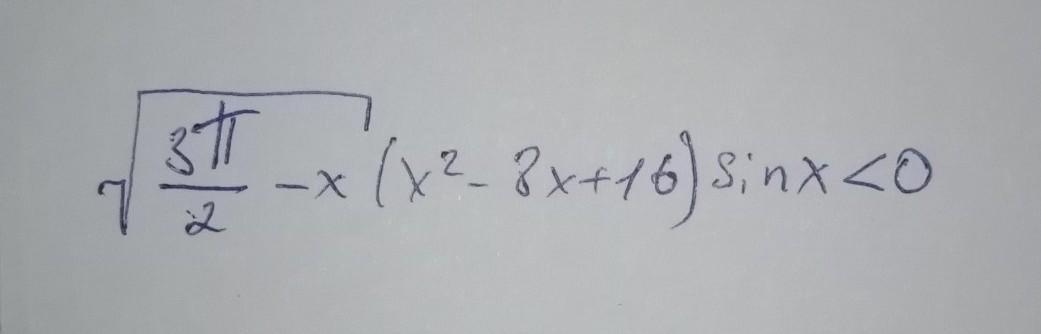
Ответы
Автор ответа:
0
Ответ:
Первые два множителя неотрицательные, но так как неравенство строгое, то они не должны равняться нулю.
Знак неравенства зависит от sinx , который отрицателен в 3 и 4 четвертях :
Но так как и
, то
Похожие вопросы
Предмет: Окружающий мир,
автор: Анэрика
Предмет: Русский язык,
автор: 10091977
Предмет: Английский язык,
автор: maryam7
Предмет: Русский язык,
автор: жексенасель
Предмет: Русский язык,
автор: Vladaije55y