Предмет: Алгебра,
автор: Paladin657
Помогите решить пожалуйста
Приложения:
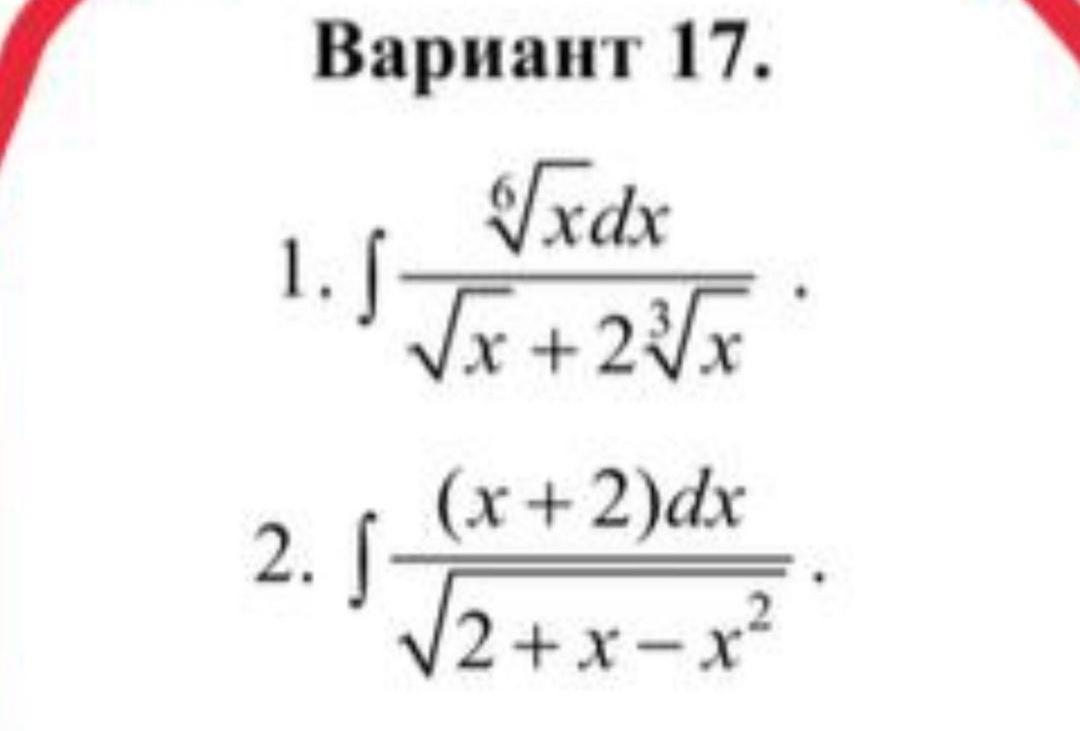
Ответы
Автор ответа:
0
Ответ:
1.
замена:
2.
В числителе делаем производную знаменателя: 1-2х
Во втором интеграле в знаменателе выделяем квадрат:
Похожие вопросы
Предмет: Русский язык,
автор: снежана92
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: ДаркаМалка
Предмет: Математика,
автор: rus179
Предмет: Математика,
автор: gggg5555666