Предмет: Геометрия,
автор: ibashmakow2007
Помогите решить задачу по геометрии
Приложения:
Ответы
Автор ответа:
3
Ответ:
Объяснение:
Заданий много, буду краток.
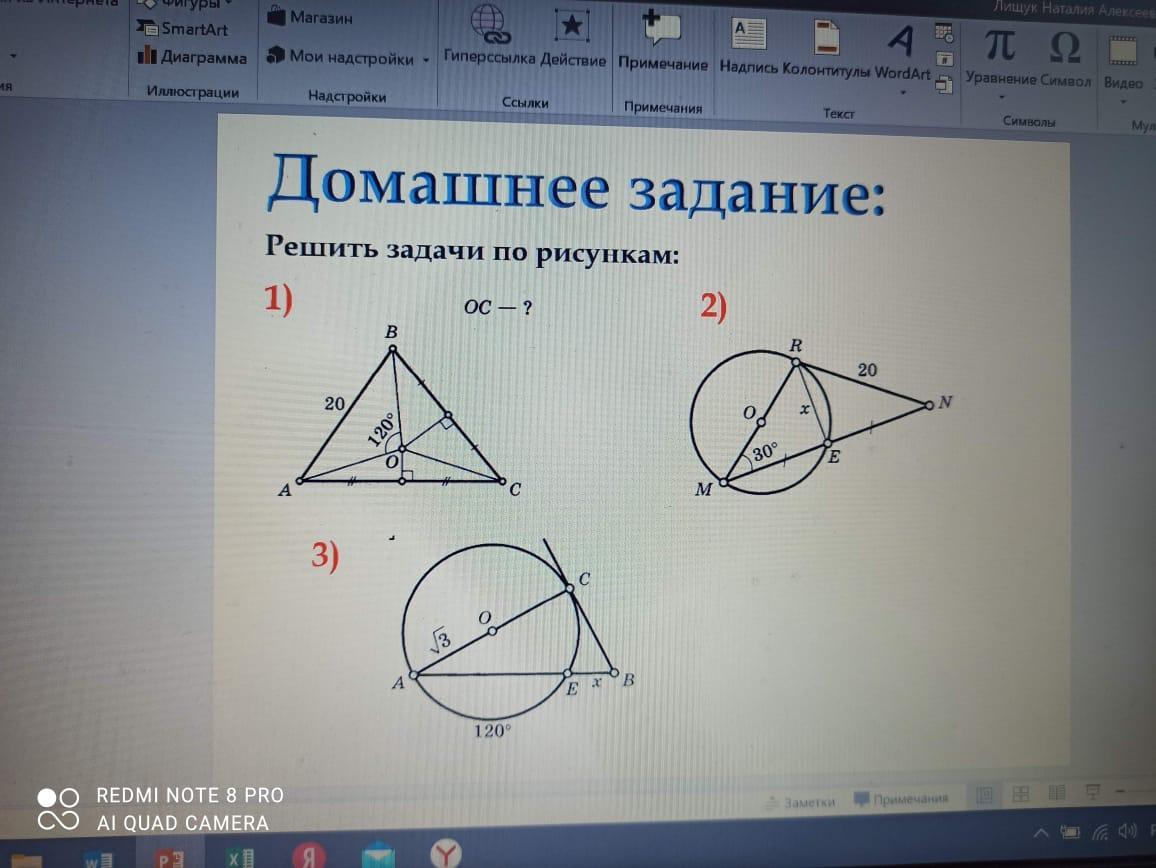
1) из рисунка т.О - точка пересечения серединных перпендикуляров => это центр описанной окружности. => OA=OB=OC, △AOB - равнобедренный, по т-ме синусов:
AO/sinABO=AB/sinAOB;
OC=AO=sinABO*AB/sinAOB=sin30°*20/sin120°=1/2*20*2/√3=20/√3
2) <MER опирается на диаметр, значит <MER=90°, тогда RE - медиана и высота => △MRN - равнобедренный. MR=RN=20
RE=1/2*MR=1/2*20=10
x=10
3) дуга СЕ=180-120=60 => <CAE=60/2=30°
△ACB - прямоугольный (радиус в точку касания)
AC=2√3
tgCAB=tg30°=BC/AC; BC=AC*tg30°=2√3/√3=2
AB=2*BC=4
BC²=EB*AB; EB=BC²/AB=4/4=1
x=1
Похожие вопросы
Предмет: Окружающий мир,
автор: svetik83
Предмет: Русский язык,
автор: look777
Предмет: Английский язык,
автор: max274
Предмет: Математика,
автор: recebova1987
Предмет: Геометрия,
автор: ник5397