Question

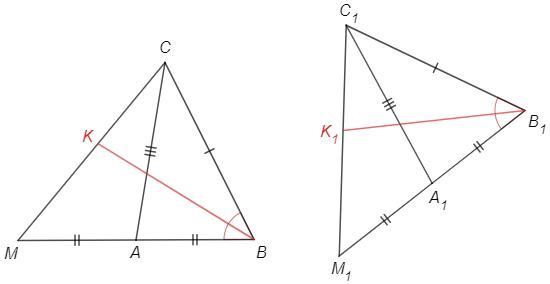
У трикутників cmb і c1m1b1,cb=c1b1,mb=m1b1,ca=c1a1.Де ca і c1a1 - медіани трикутника.Довести рівність бісектрис bk і b1k1(В треугольников cmb и c1m1b1, cb = c1b1, mb = m1b1, ca = c1a1.Де ca и c1a1 - медианы трикутника.Довесты равенство биссектрис bk и b1k1)Срочно!!!!

Answer 1

Медиана соединяет вершину треугольника с серединой противоположной стороны.

CA - медиана, A - середина MB, AB=MB/2

C1A1 - медиана, A1 - середина M1B1, A1B1=M1B1/2

MB=M1B1 => MB/2 =M1B1/2 => AB=A1B1

CB=C1B1, CA=C1A1

△ABC=△A1B1C1 (по трем сторонам)

∠ABC=∠A1B1C1 => ∠MBC=∠M1B1C1

MB=M1B1, CB=C1B1, ∠MBC=∠M1B1C1

△MBC=△M1B1C1 (по двум сторонам и углу между ними)

В равных треугольниках равны соответствующие элементы - в частности биссектрисы из соответствующих вершин, BK=B1K1.

Докажем.

MB=M1B1, ∠M=∠M1

∠MBC=∠M1B1C1 => ∠MBC/2=∠M1B1C1/2 => ∠MBK=∠M1B1K1

△MBK=△M1B1K1 (по стороне и прилежащим углам)

BK=B1K1