Предмет: Геометрия,
автор: Grrr1thefirst
ПОМОГИТЕ СРОЧНО!!!
ВСЕ УСЛОВИЕ ДАНО
Приложения:
Ответы
Автор ответа:
1
Ответ:
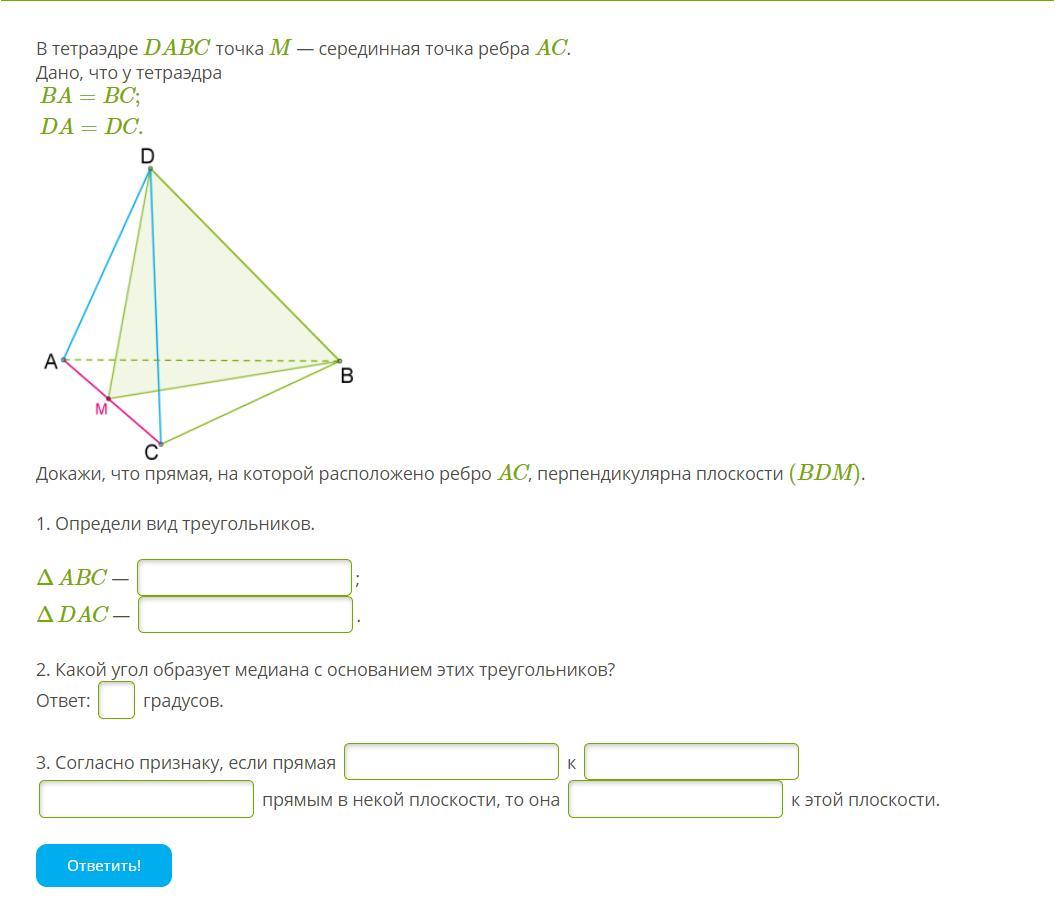
В тетраэдре DABC точка M делит пополам ребро AD. Известно, что в этом тетраэдре BA=BD;CA=CD. На рисунке . Докажи, что прямая, на которой находится ребро AD, перпендикулярна плоскости (BCM).
Объяснение:
1. В тетраэдре все боковые ребра , проведенные из вершины тетраэдра , равны. По условию BA=BD;CA=CD ,значит ΔADB –равносторонний, ΔDAC –равносторонний.
2. По свойству медианы равнобедренного треугольника , она является высотой, значит ВМ⊥ АD и СМ ⊥AD .
Поэтому угол , который образует медиана с основаниями этих треугольников равен 90°
3. Согласно признаку перпендикулярности прямой и плоскости , если прямая перпендикулярна к двум пересекающимся прямым МС и МВ , лежащим в плоскости ВСМ, то она перпендикулярна к этой плоскости (ВСМ).
Похожие вопросы
Предмет: Русский язык,
автор: девочкаприпевочкаМаш
Предмет: Окружающий мир,
автор: ученик701
Предмет: Окружающий мир,
автор: Nastyatoporkova16
Предмет: Химия,
автор: Амелия15