Question

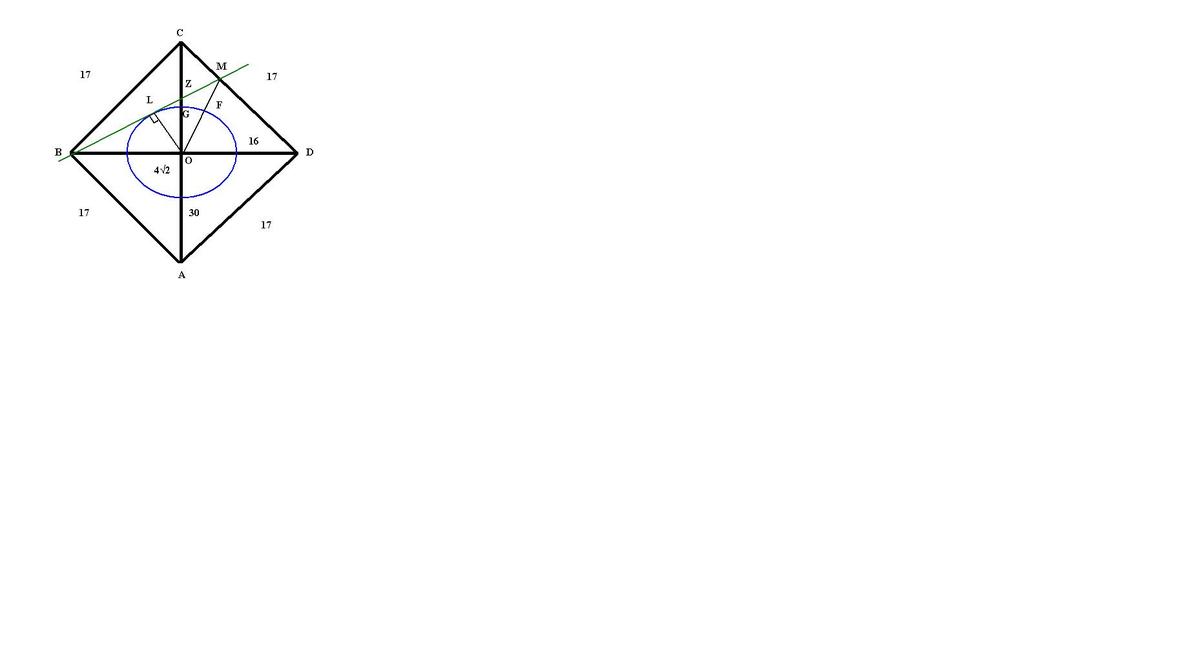
 Дан ромб ABCD с диагоналями AC=30 и BD=16. Проведена окружность радиусом 4корня из 2 с центром в точке пересечения диагоналей ромба. Прямая, проходящая через вершину В, касается этой окружности и пересекает прямую CD в точке М. Найдите СМ

Answer 1

Обозначим высоту прямоугольного треугольника $BOZ$ и он же радиус данной окружности как $OL$, где $O$ центра окружности .  Тогда   
$BL=sqrt{(frac{16}{2})^2-(4sqrt{2})^2}=4sqrt{2}$ , тогда $OL$_|_$BZ$,следует равенство $OL^2=BL*LZ\ (4sqrt{2})^2=(4sqrt{2})*LZ\ LZ=4sqrt{2}$, то есть треугольник  $BOZ$ равнобедренный, тогда угол $BZO=45а$.  
$ZO=sqrt{2*(4sqrt{2})^2}=8$ ⇒ $CZ=15-8=7$ . 
Теперь чтобы найти $CM$ есть много способов , один и них такой 
Угол $BCD$ по теореме косинусов   
$16^2=2*17^2-2*17^2*cosBCD\ cosBCD=frac{161}{289}$ 
 Далее следует такие соотношения 
$(8sqrt{2})+ZM)^2=17^2+CM^2-2*17*CM*frac{161}{289}$
$CM^2=7^2+ZM^2-14ZM*cos45$
решая систему  замена $ZM=x\ CM=z$
$z^2=49+x^2-7xsqrt{2}\ z^2=7(7-xsqrt{2})+x^2$
подставляя во второе получим что 
$z=frac{119}{23}$