Предмет: Алгебра,
автор: t8t8t853
Решите уравнение!!!!!!!!!
Приложения:
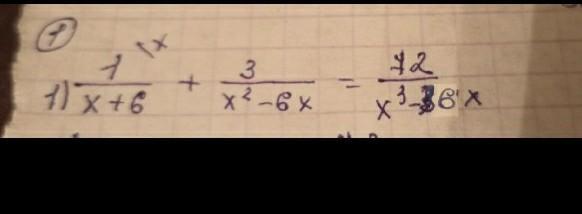
Ответы
Автор ответа:
0
Ответ:
Объяснение:
ОДЗ:
Приведем к общему знаменателю:
Теперь можно избавиться от знаменателя в уравнении, однако нужно учесть ОДЗ:
Как мы видим, один из корней, полученный при решении кв. уравнения, не входит в ОДЗ. И поэтому в ответ записываем только одно значение х.
Ответ: х = 9
Похожие вопросы
Предмет: Английский язык,
автор: valerus13
Предмет: Английский язык,
автор: lolkek19
Предмет: Английский язык,
автор: valerus13
Предмет: Физика,
автор: ксюша1773