Question

6 задание егэ. треугольник абс, угол с = 90, сн - высота, ав = 34, tgА = 1/4. найти ан. ответ: 32, прошу, объясните как :(​

Answer 1

Тангенс угла наклона прямой к оси Ох равен угловому коэффициенту к этой прямой в виде у = кх + в.

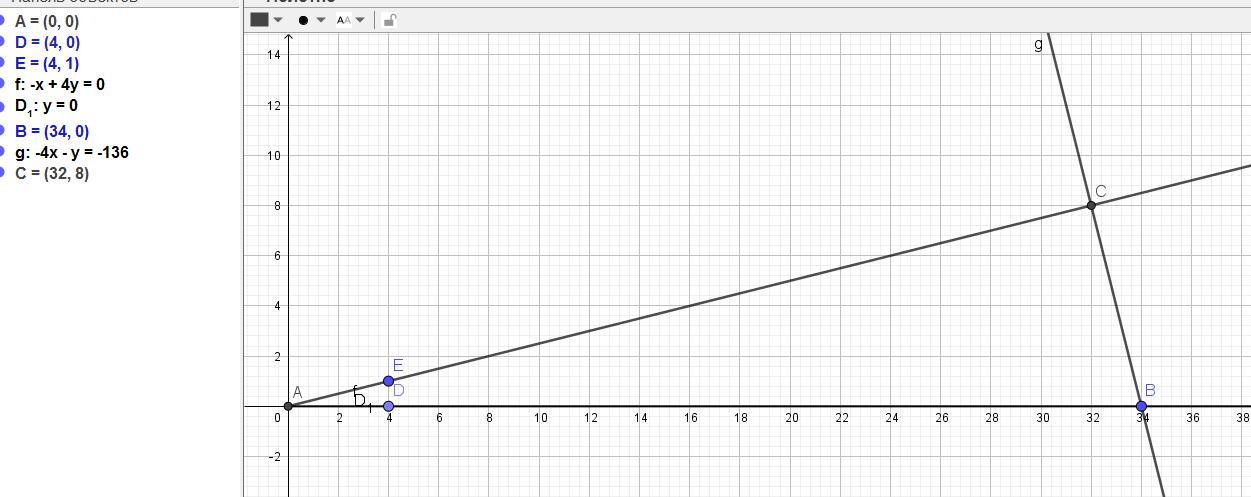
Тогда прямая АС имеет вид у = (1/4)х (в = 0, если точка А в начале координат).

Перпендикулярная прямая ВС имеет к = -1/к(АС) = -1(1/4) = -4.

ВС: у = -4х + в. Подставим координаты точки В(34; 0).

0 = -4*34 + в, отсюда в  = 4*34 = 136.

Находим координату х точки Н как абсциссу точки пересечения прямых АС и ВС:

(1/4)х = -4х + 136,

(17/4)х = 136,

х = 136*4/17 = 544/17 = 32.

Ответ: АН = 32.

Возможно более простое решение.

Пусть СН = х, АН = 4х.

Угол В = 90 - А.

tg B = ctg А, то есть tg B = 1/(1/4) = 4.

Тогда отрезок ВН = х/4.

Сторона АВ = 34 = 4х + (х/4).

Или (17/4)х = 34, откуда х = 34*4/17.

Так как АН = 4х, то получаем этот же ответ: АН = 4*34*4/17 = 32.