Предмет: Геометрия,
автор: 15galaxycat15
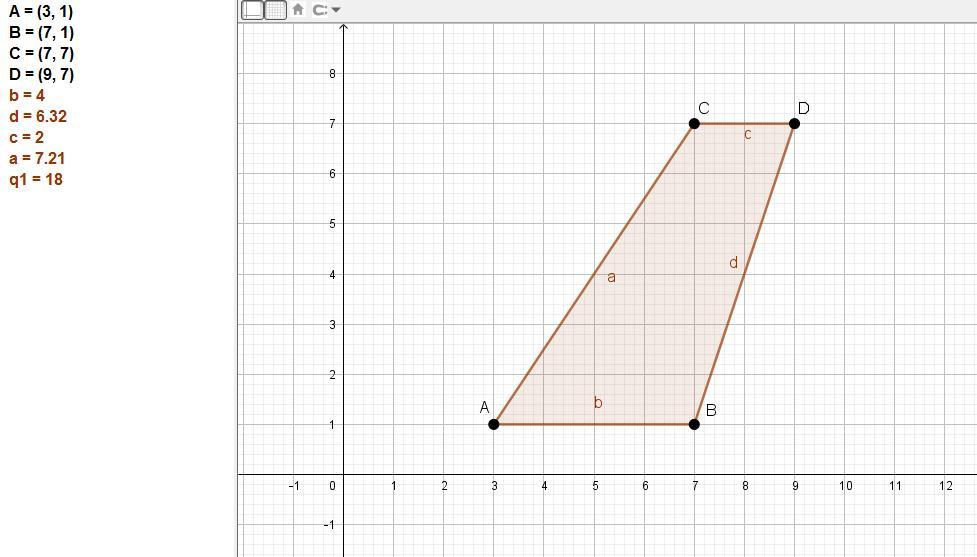
найдите площадь трапеции вершины которой имеют координаты (3;1) (7;1) (7;7) (9;7)
СРОЧНО!!!
Ответы
Автор ответа:
1
По заданным координатам видно, что основания трапеции - это отрезки АВ и СД (у них равны ординаты).
Находим высоту трапеции H = 7-1 = 6.
Средняя линия L трапеции равна:
L = (7-3) + (9-7)/2 = (4+2)/2 = 3.
Ответ: S = 6*3 = 18 кв.ед.
Если дана фигура с координатами, по которым сразу нельзя определить параметры для вычисления площади, то можно применить формулу:
Пусть (х1, y1), (x2, у2), …, (хN,уN) —координаты вершин заданного многоугольника в порядке обхода по или против часовой стрелки. Тогда его ориентированная площадь S будет равна:
S = (1/2)*(x1*y2-y1*x2+x2*y3-y2*x3+...+xn*y1-yn*x1).
Для трапеции также можно применить метод деления на треугольники.
По координатам определить длины сторон треугольников, а потом по формуле Герона найти площадь.
Приложения:
15galaxycat15:
Спасибо большое!☺️✨
Похожие вопросы
Предмет: Қазақ тiлi,
автор: dskjgfbd
Предмет: Русский язык,
автор: 123zp
Предмет: Русский язык,
автор: 2001Ваня2001
Предмет: Русский язык,
автор: almaguld
Предмет: Алгебра,
автор: ViktoriaYkimova