Решите неравенство методом интервалов:Срочно!!!!
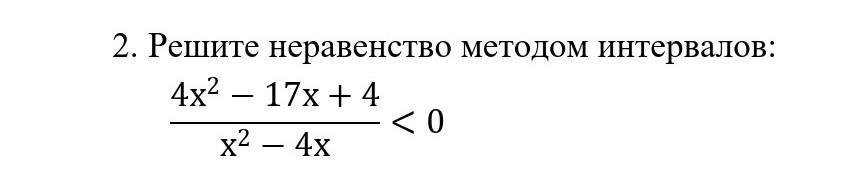
Ответы
Ответ:
В решении.
Объяснение:
(4х² - 17х + 4)/(х² - 4х) < 0
Приравнять к нулю и решить уравнение:
(4х² - 17х + 4)/(х² - 4х) = 0
4х² - 17х + 4 = 0
D=b²-4ac =289 - 64 = 225 √D=15
х₁=(-b-√D)/2a
х₁=(17-15)/8
х₁=2/8
х₁=0,25;
х₂=(-b+√D)/2a
х₂=(17+15)/8
х₂=32/8
х₂=4;
Знаменатель:
х² - 4х = 0 неполное квадратное уравнение
х(х - 4) = 0
х₃ = 0;
х - 4 = 0
х₄ = 4.
Отметить все корни схематично на числовой прямой:
________________________________________________________
-∞ + 0 - 0,25 + 4 + +∞
Определить знак самого правого интервала:
х = 5;
(4*25 - 17*5 + 4)/(25 - 20) = 19/5 > 0, значит, плюс.
Так как неравенство < 0, решения - интервалы со знаком минус.
Решение неравенства: х∈(0; 0,25).
Неравенство строгое, скобки круглые.