Предмет: Алгебра,
автор: Dima56779
Решите тригонометрическое уравнение 80б
Приложения:
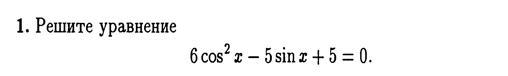
cathetinka:
это решается, но я не могу прикрепить фото с решением так как уже есть 2 ответа
кароче
6cos^x-5sinx+5=0
(нужно расписать цифру 5 как -6 и 11(в сумме будет 5) чтобы потом сократить с косинусом)
6cos^2x-5sinx-6(cos^2x+sin^2x)+11=0
6cos^2x-5sinx-66cos^2x-6sin^2x+11=0
(сокращаем 6cos^2x и -6cos^2x)
-6sin^2x-5sinx+11=0
(умножим эту часть на -1 чтобы убрать минус в начале)
6sin^2x+5sinx-11=0
(заменим sin^2x на t^2, a sinx на t, получаем квадратное уравнение)
6cos^x-5sinx+5=0
(нужно расписать цифру 5 как -6 и 11(в сумме будет 5) чтобы потом сократить с косинусом)
6cos^2x-5sinx-6(cos^2x+sin^2x)+11=0
6cos^2x-5sinx-66cos^2x-6sin^2x+11=0
(сокращаем 6cos^2x и -6cos^2x)
-6sin^2x-5sinx+11=0
(умножим эту часть на -1 чтобы убрать минус в начале)
6sin^2x+5sinx-11=0
(заменим sin^2x на t^2, a sinx на t, получаем квадратное уравнение)
6t^2+5t-11=0
D=25+264=289, корень дискриминанта 17
t1=-5+17/12=1
t2=-5-17/12=-11/6
1)sinx=-11/6
так как -11/6>1, то x не существует
2)sinx=1
x=пи/2+2пи*n, n€Z
D=25+264=289, корень дискриминанта 17
t1=-5+17/12=1
t2=-5-17/12=-11/6
1)sinx=-11/6
так как -11/6>1, то x не существует
2)sinx=1
x=пи/2+2пи*n, n€Z
там где t1 и t2 -5-17 и -5+17 пиши сверху дроби а 12 снизу
в конце -11/6>1 это знак больше, тут почему то он не отображается
Ответы
Автор ответа:
0
Ответ:
n€Z
Объяснение:
основные тригонометрическое тождество:
тригонометрическое квадратное уравнение, замена переменной:
t1=-22/12 - посторонний корень
обратная замена:
Похожие вопросы
Предмет: Английский язык,
автор: 111111111111111117
Предмет: Українська мова,
автор: елизавета59
Предмет: Английский язык,
автор: дианочка74
Предмет: Математика,
автор: света1189