Предмет: Геометрия,
автор: timurovnodir52
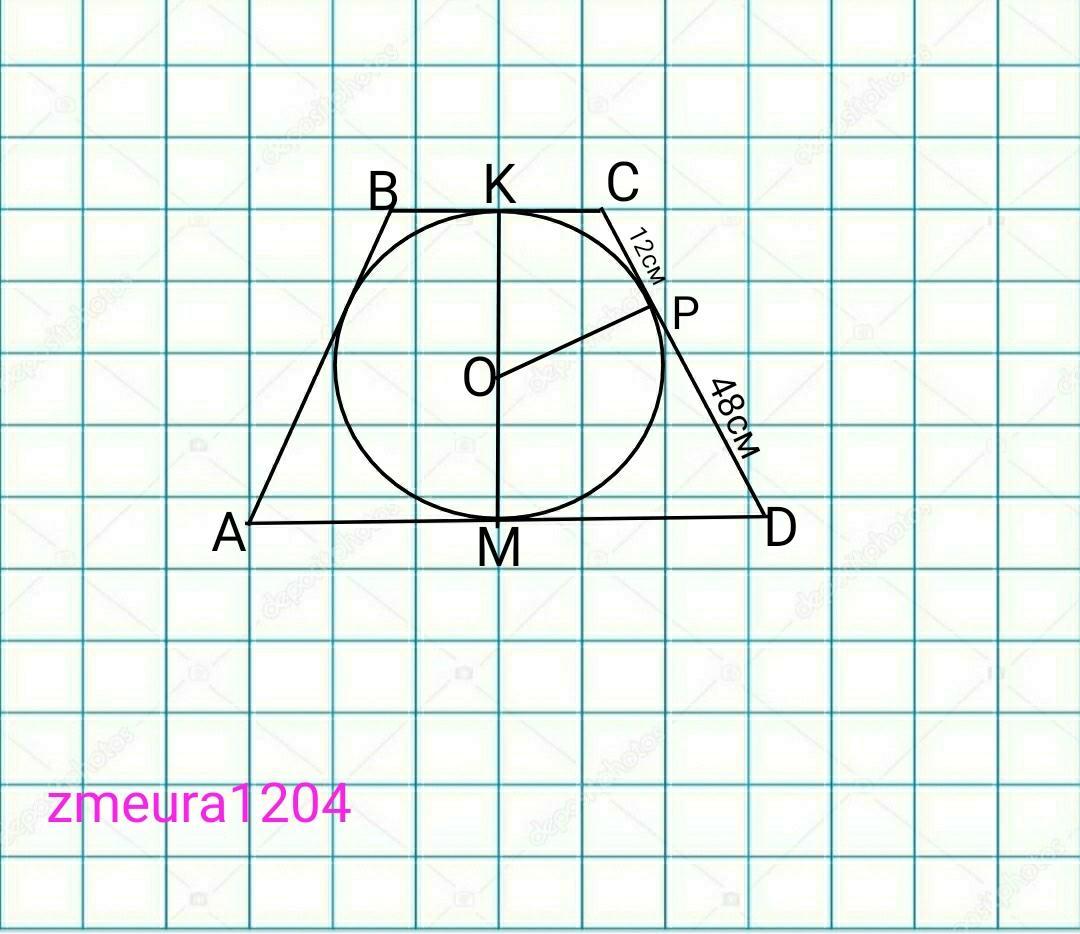
в равнобокой трапецию вписана окружность. боковык стороны трапеции делятчя точкой касания окружности на отрезки длиной 12 см и 48 см. найти отношения площади трапеции к площади круга
Ответы
Автор ответа:
3
Ответ:
5/π
Объяснение:
r=√(CP*PD)=√(12*48)=√576=24см
Sкр=πr²=24²π=576π см²
KM=2r=2*24=48см. высота трапеции
(BC+AD)=(CD+AB)
CD=AB
(BC+AD)=2*CD
(BC+AD)=(12+48)*2=120 сумма оснований трапеции
Sтр=h(a+b)/2, формула нахождения площади трапеции, h-высота; а;b- основания
Sтр=КМ(ВС+АD)/2=48*120/2=48*60=2880 см²
Sтр/Sкр=2880/576π=5/π
Приложения:
zcom2113:
zmeura1204,здравствуйте, вы мне не поможете, пожалуйста с математикой???Задания у меня в профиле)))
В трапецию вписана окружность ВС+АD=AB+CD.
Всё на покой.
Всё исправила.
zmeura1204,здравствуйте, вы мне не поможете, пожалуйста с математикой???
Похожие вопросы
Предмет: Русский язык,
автор: Svetlana20062901
Предмет: Другие предметы,
автор: Дашулька4444
Предмет: Русский язык,
автор: Анастасия2903
Предмет: Русский язык,
автор: olafanaskin201