Предмет: Математика,
автор: rinnitan04200601
Пожалуйста, помогите мне решить, дам 80 баллов. Пожалуйста помогите
Приложения:

Ответы
Автор ответа:
8
1.
1)
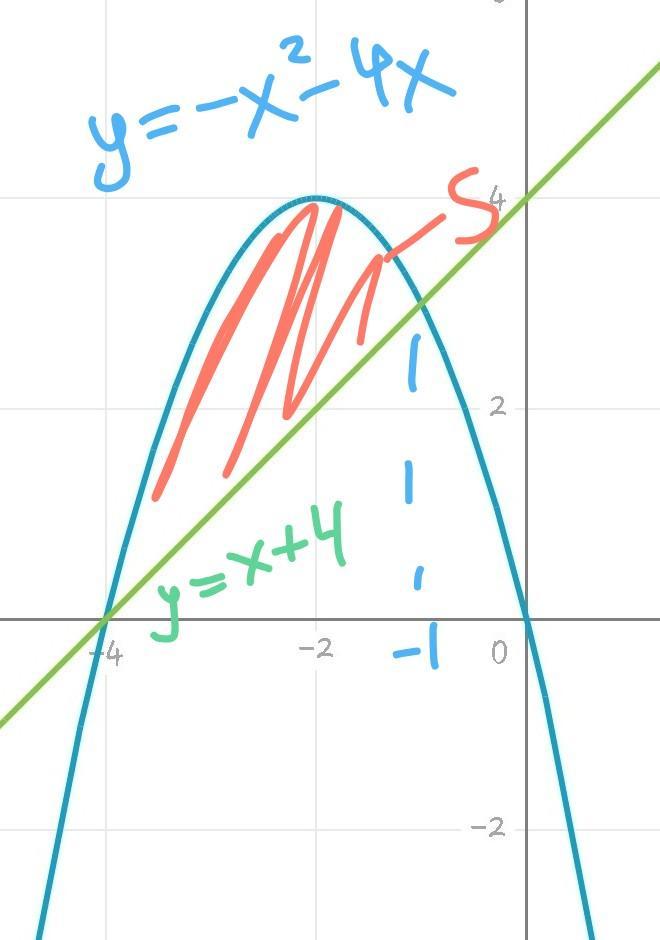
Найдем точки пересечения
рисунок
Ответ: 4,5
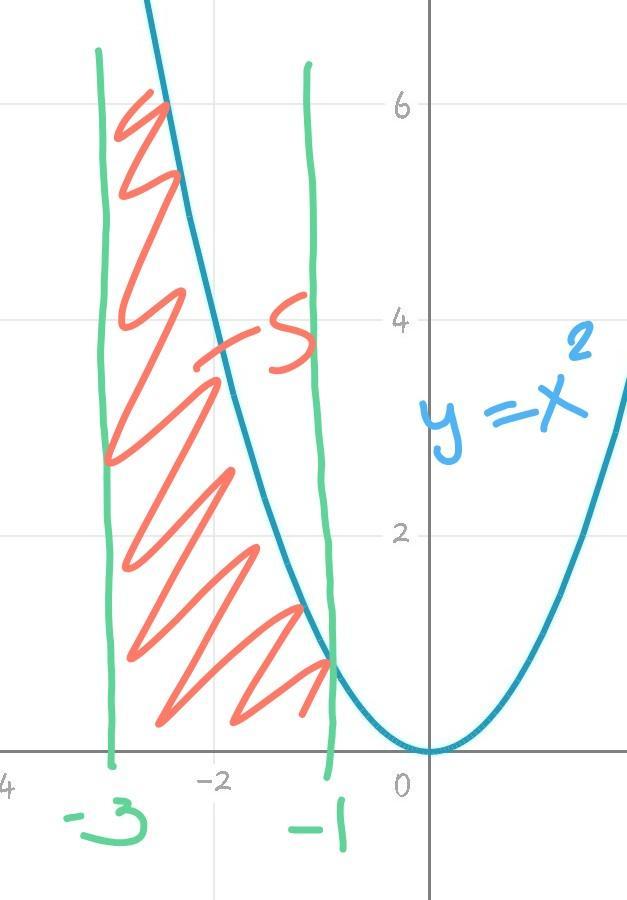
2)
рисунок
2.
1.
2.
3.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: klaravinnik
Предмет: Окружающий мир,
автор: Аноним
Предмет: Музыка,
автор: tairon1
Предмет: Литература,
автор: шуруша
Предмет: Математика,
автор: Sasha20th
https://znanija.com/task/44735035