Предмет: Математика,
автор: milaya139
Диференційне рівняння
Допоможіть з вирішенням
Приложения:
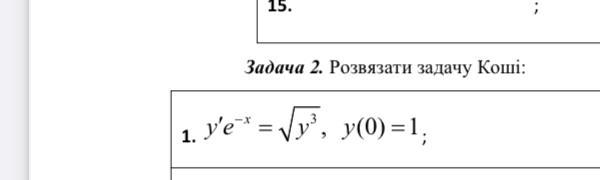

Ответы
Автор ответа:
2
1)
Найдем C, используя начальные условия y(0)=1:
Ответ:
2)
В процессе решения при делении на (2y+1) было потеряно решение y=-1/2. Оно вписывается в общее решение, если подставить
Окончательный ответ:
milaya139:
Спасибо
Похожие вопросы
Предмет: Русский язык,
автор: 78mm78kk
Предмет: Физика,
автор: verakiriltseva
Предмет: Русский язык,
автор: pienkova04
Предмет: Русский язык,
автор: Katyallll
Предмет: Математика,
автор: Черепашка1703