помогите СООООООООР!!!!!!

Ответы
Чтобы обосновать ответ, нужно решить каждое из неравенств
a) 2-9x+23≥0
2-9x+23=0
D=(-9)²-4·2·23
D=-103
Дискриминант отрицательный, корней нет
Если нет корней, а коэффициент a>0, левая часть неравенства положительна, значит, что утверждение истинно для любого значения x
x∈R
Ответ: 2. Решением неравенства является вся числовая прямая
b) -x²+14x-49>0
-x²+7x+7x-49>0
-x(x-7)+7(x-7)>0
-(x-7)(x-7)>0
-(x-7)²>0
(x-7)²<0
Левая часть неравенства всегда будет положительна или равна 0, значит, что утверждение ложно для любого значения x
x∈∅
Ответ: 1. Неравенство не имеет решений
c) x²-6x+5≤0
x²-6x+5≤0
D=(-6)²-4·1·5
D=16
x=-(-6)±√16 / 2·1
x=6±4 / 2
x₁ = =
= 5
x₂ = =
= 1
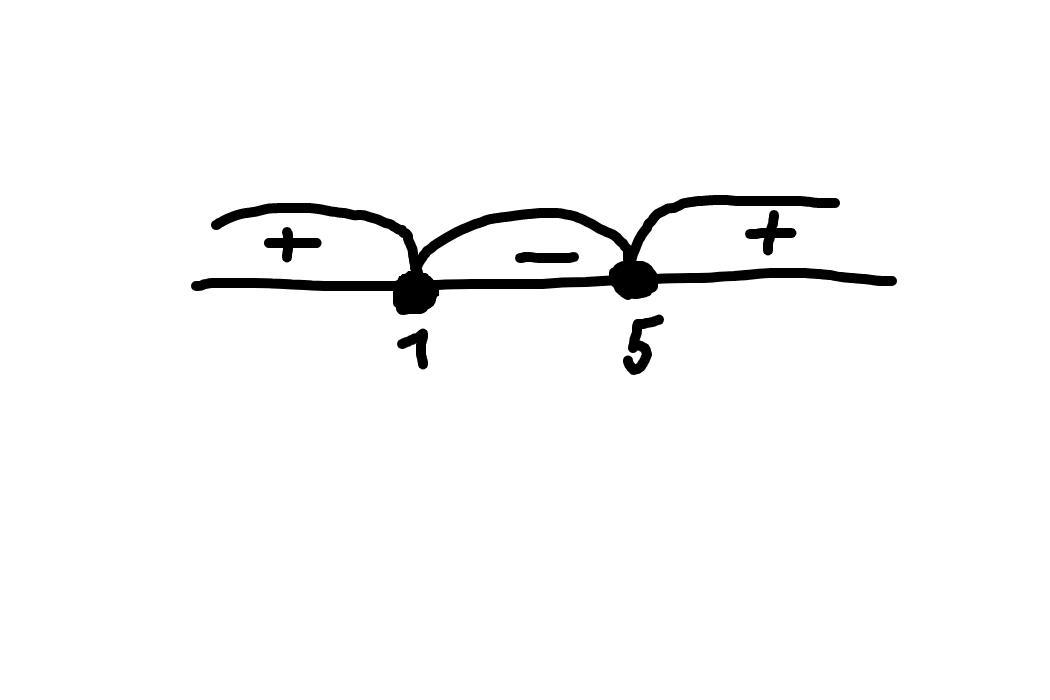
Неравенство не строгое, значит точки закрашенные.
Чтобы поставить промежутки, проверим с помощью функции. Для этого возьмём любое число больше самой правой точки, т.е. в нашем случае x>5
x=6
f(x)=6²-6·6+5
f(x)=36-36+5
f(x)=5>0
Самый правый промежуток положительный, остальные чередуются плюс-минус-плюс.
Нам нужно всё, что меньше. Это промежуток от 1 до 5.
x∈[1;5]
Ответ: 4. Решением неравенства является закрытый промежуток
d) -x²+16<0
-x²+16=0
-x²=-16
x²=16
x=±4
x₁ = -4
x₂ = 4
Неравенство строгое, значит точки выколотые. a<0 значит промежутки чередуются минус-плюс-минус. Нам нужно всё, что меньше. Это объединение двух промежутков:
x∈(-∝;-4)∪(4;+∝)
Ответ: 6. Решением неравенства является объединение двух промежутков.
Все интервалы в прикреплённых файлах.
Удачи!