Question

Дам 50 балоов!!!!Помогитеее!!!!!​

Answer 1

Ответ:

1.

$(x - 3)(x - 4) < 0 \\ \\ x - 3 = 0 \\ x = 3 \\ \\ x - 4 = 0 \\ x = 4 \\ \\ + \: \: \: \: - \: \: \: \: \: \: \: \: + \\ - - 3- - 4 - - > \\ x\in(3;4)$

Ответ: С

2.

$y = {x}^{2} - 2x - 8 \\ \\ {x}^{2} - 2x - 8 = 0 \\ D= 4 + 32 = 36 \\ x_1 = \frac{2 + 6}{2} = 4 \\ x_2 = - 2$

рисунок

Здесь непонятно, какие решения искать.

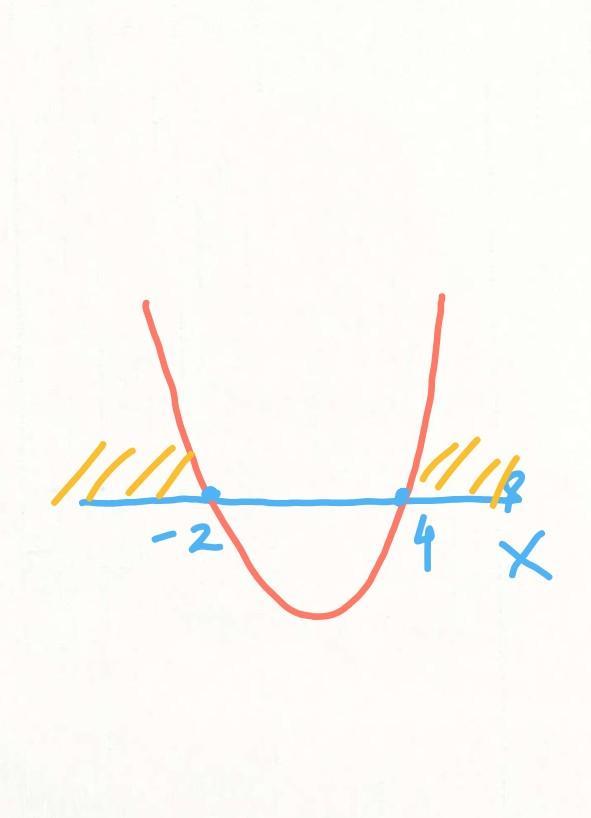
1. Если < 0

х ∈ (-2; 4), ответ А

2. Если <=0

х ∈ [-2; 4], ответ В

3. Если >=0

х∈ (- беск; -2]U[4; + беск), ответ D

3.

${x}^{2} - 3x - 10 < 0 \\ D = 9 + 40 = 49 \\ x_1 = \frac{3 + 7}{2} = 5 \\ x_2 = - 2 \\ + \: \: \: \: \: \: \: \: - \: \: \: \: \: \: \: + \\ - -( - 2) - - 5 - - > \\ x\in( - 2;5)$

4.

$\left \{ {{0.5x {}^{2} - x - 4 \geqslant 0} \atop {2 - 3(x - 4) > 4x} } \right. \\ \\ 1)0.5 {x}^{2} - x - 4 \geqslant 0 \: \: \: | \times 2 \\ {x}^{2} - 2x - 8 \geqslant 0 \\ ( x+ 2)(x - 4) \geqslant 0 \\ + \: \: \: \: \: - \: \: \: \: \: \: + \\ - - ( - 2) - - 4 - - > \\ x\in( - \infty; - 2]U[4; + \infty ) \\ \\ 2)2 - 3(x - 4) > 4x \\ 2 - 3x + 12 > 4x \\ - 7x > - 14 \\ x < 2$

Пересекаем оба решения

Ответ:

$x\in( - \infty; - 2]$

5.

$\frac{ {x}^{2}(1 - x) }{ {x}^{2} - 14x + 49 } \leqslant 0 \\ \\ x = 0 \\ \\ 1 - x = 0 \\ x = 1 \\ \\ {x}^{2} - 14x + 49 = 0 \\ (x - 7) {}^{2} = 0 \\ x = 7 \\ \\ \frac{ {x}^{2}(1 - x) }{ {(x - 7)}^{2} } \leqslant 0 \\ \\ + \: \: \: \: \: \: \: + \: \: \: \: \: \: \: - \: \: \: \: \: \: \: \: \: \: \: - \\ - -0 - - 1 - -7 - - >$

Ответ: х ∈ {0}U[1;7)U(7; + беск)

6.

$\left \{ {{x {}^{2} - 5x + 11 > 0 } \atop { {x}^{2} \leqslant 64} } \right. \\ \\ 1) {x}^{2} - 4x + 11 > 0 \\ D= 16 - 44 < 0$

корней нет, парабола выше оси ОХ => х∈ R

$2) {x}^{2} \leqslant 64 \\ {x}^{2} - 64 \leqslant 0 \\ (x - 8)(x + 8) \leqslant 0 \\ + \: \: \: \: \: - \: \: \: \: \: \: + \\ - -( - 8) - - 8- - - > \\ x\in[ - 8;8]$

Ответ:

$x\in[- 8;8]$