Предмет: Геометрия,
автор: МирзаевФайк
В прямоугольном треугольнике ABC (C = 90 °) AB = 20 ° ABC = 30 °. Если круг был нарисован так, что точка А является точкой центра . Каков радиус круга было бы если:
а) круг касается прямой BC;
б) если окружность не имеет общих точек с прямой BC;
в)круг пересекает прямую BC в двух точках.
justvanyok:
аааа
АС напротив угла 30 градусов...
на дано похоже
Где-то я такое уже решала.
Гдето на знаниях
Да.
Надо так понимать, что AB = 20, угол ABC = 30 °
Ответы
Автор ответа:
4
Ответ:
Объяснение:
Решение ∆АВС, АВ=20; <С=90; <В=30
=> АС=10.
1. Окружность радиусом Ар касается прямой ВС, точка касания С,.
=> R= AC =10.
2,окружность Ar не пересекает прямую ВС, => Ar < 10
3 окружность пересекает ВС в двух точках , => Ar > 10
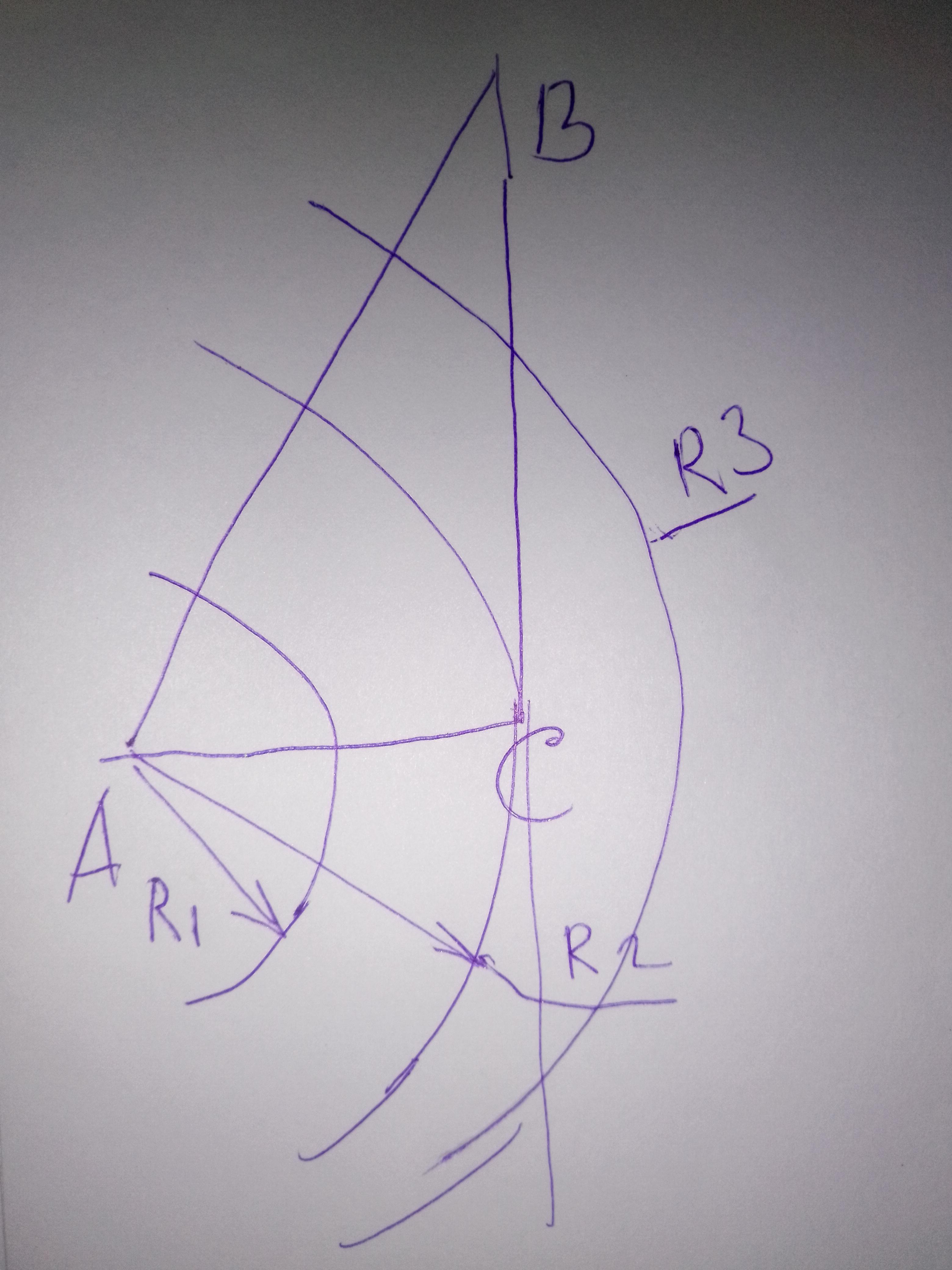
Картинки к каждому нарисуй самостоятельно
Радиусы пронумерованы соответственно для каждого из условий, если подумать то могли бы и сами , рисовал на коленке поэтому косовато но смысл думаю ясен
Приложения:
Что да?
Все комментарии удалили...
Это же хорошо.
<АВС=30 по заданию
Похожие вопросы
Предмет: Русский язык,
автор: айдамир2
Предмет: Математика,
автор: лашенькамоясобачка
Предмет: Литература,
автор: Аноним
Предмет: Литература,
автор: denis1590
Предмет: Математика,
автор: WolfY90