Помогите пожалуйста!

Ответы
Ответ и решение на фото

Ответ:
AY = 12√3
Пошаговое объяснение:
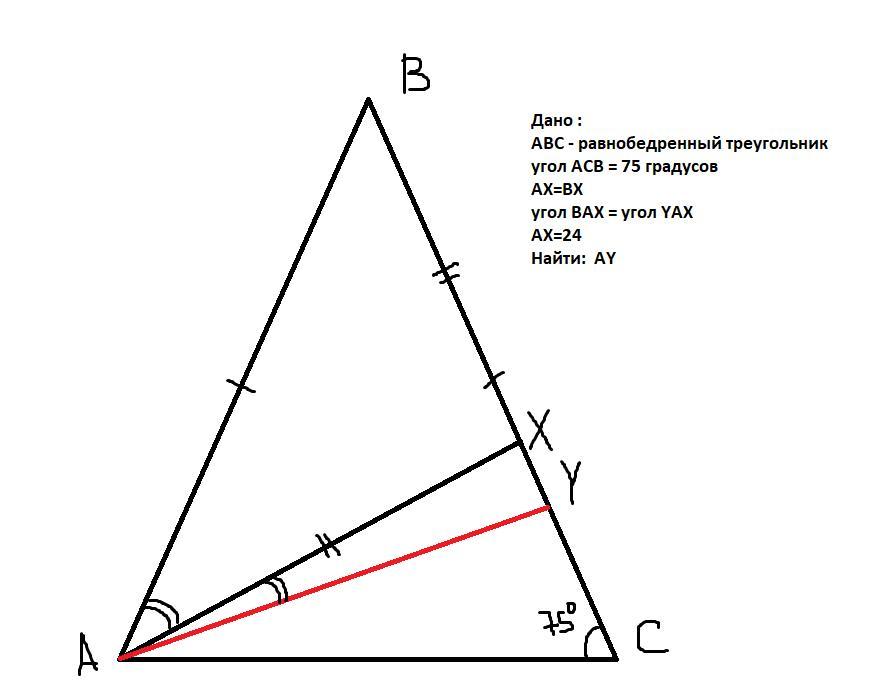
Рассмотрим равнобедренный треугольник ΔABC:
Так как ∠ ACB = 75° ,то и второй угол при основании ∠BAC = ∠ ACB = 75°
Тогда угол ∠ABC при вершине равен разности 180° и сумме двух углов при основании AC ,т.е. :
∠ABC = 180° - (∠BAC+∠ ACB) => ∠ABC = 180° - 150° = 30°
Далее,рассмотрим другой равнобедренный треугольник ΔAXB:
Так как ∠ABC = 30°,то и ∠ABX = ∠ABC = 30° значит ,т.к. ΔAXB есть равнобедренный треугольник,то ∠BAX = 30° ,тогда найдём угол ∠AXB:
∠AXB = 180° - (∠ABX+∠BAX ) = 180° - 60° = 120°.
Заметим,что ∠BAX смежен с ∠YAX и при этом равны ∠BAX = ∠YAX = 30°
Далее, ∠AXB смежен с ∠AXY ,то по свойству смежных углов:
∠AXY = 180°-∠AXB =>∠AXY= 180°-120° = 60°
Рассмотрим теперь ΔXAY :
Так как ∠YAX = 30° и ∠AXY= 60° ,то найдём и третий угол ∠AXY :
∠AXY = 180° - (∠YAX+∠AXY) = 180°-90°=90°
Соответственно ΔXAY - прямоугольный
Так как AX = 24 ,а ∠YAX = 30° ,то найдём AY по косинусу:
cos 30° = AY /24 = > AY = 24* √3/2 = 12√3
Задача решена!