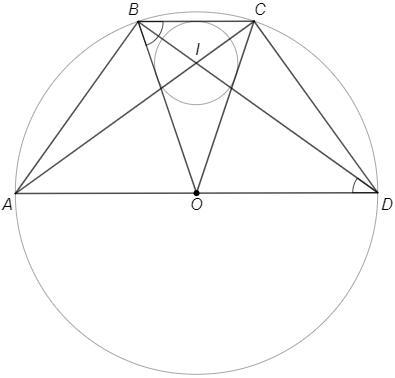
Равнобокая трапеция ABCD вписана в окружность с диаметром AD и центром в точке O. В треугольник BOC вписана окружность с центром в точке I. Найдите отношение площадей треугольников AID и BIC, если известно, что AD=27, BC=3.
Ответы
Ответ:
9
Объяснение:
1.треугольники AID и CIB подобны по всем равным углам (вертикальные + накр. леж. углы)
Также треугольники ABI и DCI равны
=> AI=DI и BI=IC
=> треугольники AID и CIB равнобедренны
2. Т.к. треугольники подобны, то все отношения сторон равны 1:3
Это значит, что при составлении пропорции площадей, мы получим примерно такое отношение:
(3a * 3h):2 / (a * h):2
=>
(3a * 3h):2 / (a * h):2 =
= 3a * 3h * 2 / 2 * a * h =
2 и ah сокращается и мы получаем в результате, что отношение площадей будет равно 9
OB=OD (радиусы) => △BOD - равнобедренный => ∠OBD=∠ODB
∠CBD=∠ODB (накрест лежащие при BC||AD)
=> ∠OBD=∠CBD, BD - биссектриса ∠CBO
Аналогично CA - биссектриса ∠BCO
Центр вписанной окружности - пересечение биссектрис
=> точка I - пересечение BD и CA.
△AID~△BIC (по накрест лежащим при BC||AD)
S(AID)/S(BIC) = (AD/BC)^2 = (27/3)^2 =9/1