Question

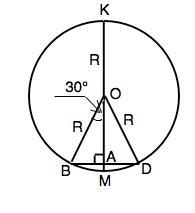
3. В окружности с центром О проведен диаметр KM-14,4см, пересекающий хорду BD в точке
А, причем А середина хорды. Угол между диаметром и радиусом равен 30° Найдите длину хор-
ды BD и периметр двор
​

Answer 1

Ответ: 21,6 см

Объяснение:

Соединив концы хорды с центром окружности, получим ∆ ВОD.

BO=DO=R => ∆ ВОD – равнобедренный.

R=d/2=14,4:2=7,2 (см)

Точка А - середина хорды, поэтому ОМ - медиана ∆ ВОD, =>

ОМ - высота и биссектриса   равнобедренного  ∆ ВОD.

Тогда угол ВОD=2•30°=60°, =>

углы при основании BD=60°.

Треугольник ВОD- равносторонний. ВD=DO=BO=R

BD=7,2 см

Р(∆ DBO)=3•7,2=21,6 см