Question

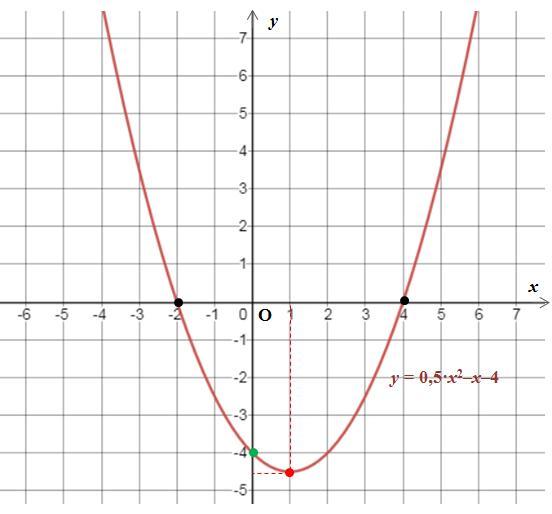
2. Используя график функции y=0,5x^2-x-4 найдите решение неравенства 0,5x^2

HELLLP

Answer 1

Ответ:

D) (−∞; –2] ∪ [4; +∞)

Объяснение:

Полное условие: 2. Используя график функции y=0,5•x²–x–4 найдите решение неравенства 0,5•x²–x–4 ≥ 0.

Решение.

График функции f(x) = 0,5•x²–x–4 - это парабола. Для построения графика параболы достаточно 3 точки, одна из которых вершина параболы (красная точка).

Абсциссу вершины параболы y=a•x²+b•x+c определяем по формуле:

$\displaystyle \tt x_{0} =-\dfrac{b}{2 \cdot a} .$

Так как a = 0,5 и b = -1, то

$\displaystyle \tt x_{0} =-\dfrac{-1}{2 \cdot 0,5} = 1.$

Тогда ордината вершины параболы:

f(1) = 0,5•1²–1–4 = 0,5–5= –4,5.

Определяем точки пересечения графика с осью Ох (чёрные точки):

f(x)=0 ⇔ 0,5•x²–x–4=0 ⇔ x²–2•x–8=0 ⇔ x²+2•x –4•x–8=0 ⇔

⇔ x•(x+2) –4•(x+2)=0 ⇔ (x+2)•(x–4)=0 ⇔ x₁ = –2, x₂ = 4.

Определяем точку пересечения графика с осью Оу (зелёная точка):

f(0) = 0,5•0²–0–4 = –4.

График функции в приложенном рисунке.

Так как f(x) ≥ 0 означает, что значения функции не ниже оси Ох, то по графику определяем множество решений неравенства f(x) ≥ 0:

(−∞; –2] ∪ [4; +∞).