Предмет: Математика,
автор: evangelina4919
y’’ = y’/x + x
2(xy’+y) = xy^2
Приложения:
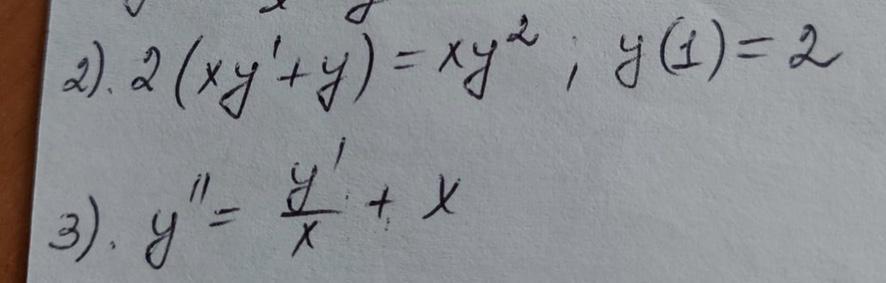
evangelina4919:
Мне нужен хотя в 1 из примеров до 13.50
Ответы
Автор ответа:
2
найдем С, используя начальные условия: x=1; y=2;
Похожие вопросы
Предмет: Математика,
автор: StellaSarah99
Предмет: Английский язык,
автор: настя20155
Предмет: Математика,
автор: cool53
Предмет: Другие предметы,
автор: Чабуречек
Предмет: Английский язык,
автор: привнтиатв