Question

Используя график функции у=х^2-2х+3,найдите решение неравенства х^2-2х-3>0

A)(-1;3)
B)(-••;-1)u(3;••)
C)(-••;2)
D)(-••;-1)|u|3;••)
E)|-1;3|
Пожалуйста ответьте на мой вопрос!!!Если не знаете, не отвечайте(

Answer 1

Ответ:

B) (-∞; -1) ∪ (3; +∞)

Объяснение:

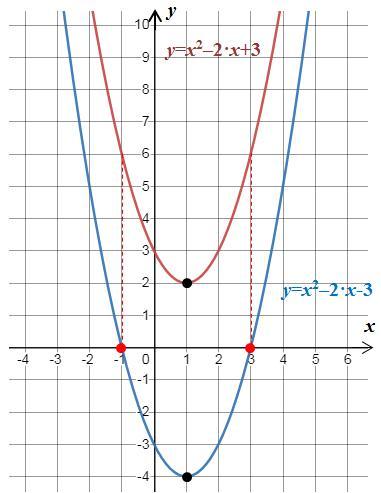
Условие неполное: не хватает рисунка с график функции у=x²-2·x+3.

Рисунок в приложении.

Решение. Для решения неравенства x²-2·x-3 > 0 используем график функции у=x²-2·x+3 (тёмно-красный график). Так как

x²-2·x-3 = (x²-2·x+3)-6 = y-6, то

график функции у=x²-2·x+3 нужно опустить его на 6 единиц вниз (синий график).

Условие x²-2·x-3 >0 означает, что график функции строго выше оси Ох. Получаем x∈(-∞; -1) ∪ (3; +∞).