Предмет: Геометрия,
автор: 1kama2
Повторение. Площади четырёхугольников и треугольников
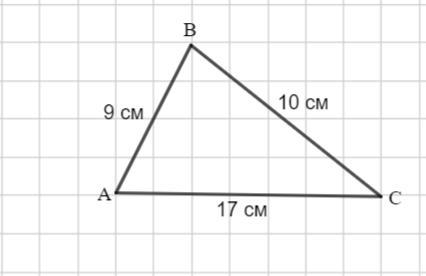
В треугольнике ABC, AB = 9 см, BC = 10 см и AC = 17 см. Найди значение синуса наименьшего угла треугольника.
Ответ:
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Напротив меньшей стороны лежит меньший угол. Так как сторона АВ наименьшая, то ∠С- наименьший.
1 способ.
Применим теорему косинусов и найдем косинус угла С.
Квадрат любой стороны равен сумме квадратов двух других сторон минус удвоенного произведение этих сторон на косинус угла между ними.
Воспользуемся основным тригонометрическим тождеством и найдем синус угла.
Синус угла в треугольнике принимает положительное значение
2 способ.
Найдем площадь треугольника по формуле Герона:
где p- полупериметр , a,b,c- стороны треугольника.
Найдем площадь этого же треугольника по формуле.
Приложения:
Похожие вопросы
Предмет: География,
автор: ivanova910
Предмет: Литература,
автор: 25103
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: алекс4531