Предмет: Алгебра,
автор: Аноним
Дифференциальное уравнение первого порядка
Приложения:
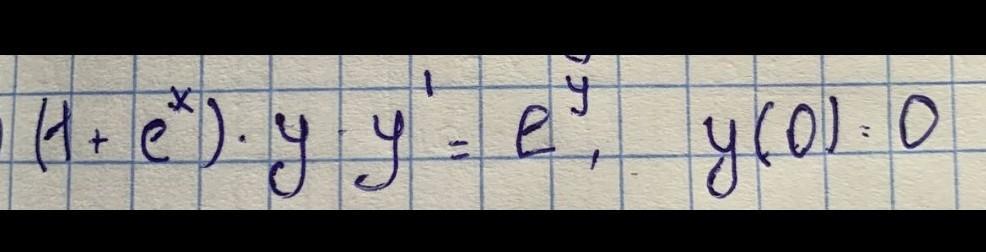
Ответы
Автор ответа:
1
Ответ:
NNNLLL54:
кнопочки нажимай
Похожие вопросы
Предмет: Обществознание,
автор: vvvvvs
Предмет: Химия,
автор: vika1117
Предмет: Математика,
автор: Victoria222
Предмет: Математика,
автор: nikeskov
Предмет: Русский язык,
автор: Впо124