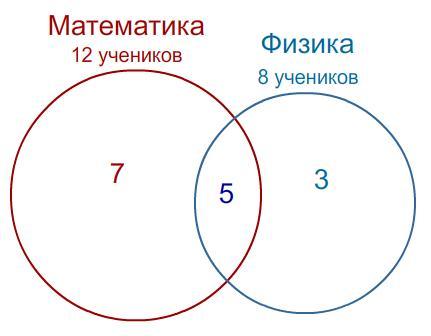
Учащиеся 10 класса приняли участие в предметных олимпиадах, причем каждый ученик участвовал либо по математике, либо по физике. Известно, что в олимпиаде по математике участвовало 12 учащихся, а по физике – 8 учащихся. 5 учащихся приняли участие в олимпиаде по двум предметам. Сколько всего участников олимпиады?
Реши задачу, используя диаграмму Эйлера-Венна.
Ответ:
.
Ответы
Ответ:
Всего 15 учеников приняли участие в олимпиаде.
Пошаговое объяснение:
В множество принявших участие в олимпиаде по математике входят 12 учеников, в множество принявших участие в олимпиаде по физике входят 8 учеников.
Известно, что 5 учащихся приняли участие в олимпиаде по двум предметам.
Пересечением множеств называют множество, в которое входят элементы, одновременно принадлежащие всем данным множествам.
Тогда пересечением множеств участников математической олимпиады и физической олимпиады является количество учеников, принявших участие в обеих олимпиадах, то есть 5.
Из 12 участников математической олимпиады 7 не принимали участие в олимпиаде по физике: 12 -5 = 7.
Из 8 участников физической олимпиады 3 не принимали участие в олимпиаде по математике: 8 -5 = 3.
А всего участников олимпиады:
7 + 5 + 3 = 15.