Трикутник АВС прямокутний,кут С=90°(мал.33).Знайти х. Рисунок (б,в).
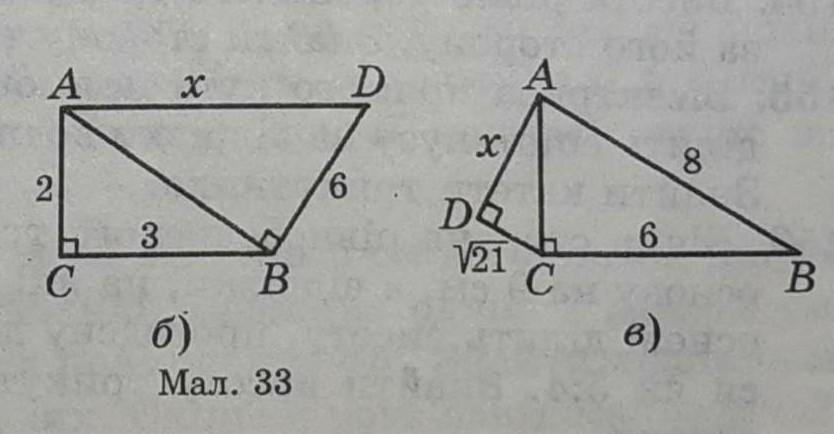
Ответы
Ответ:
Б --- 7см В --- √7см
Объяснение:
Малюнок Б
- Знайдемо довжину сторони АВ
Розглянемо трикутник АСВ - він прямокутний а значить АВ його гіпотенуза. Звідси за теоремой Піфагора (сумма квадратів катетів дорівнює квадрату гіпотенузи)
АС²+СВ²=АВ² → АВ²=2²+3² → АВ²=13 → АВ=√13
- Знайдемо сторону АD або х
Розглянемо трикутник АВD - він прямокутний а значить АD його гіпотенуза. Звідси за теоремой Піфагора (сумма квадратів катетів дорівнює квадрату гіпотенузи)
AB²+BD²=AD² → AD²=(√13)²+6² → AD²=49 → AD= 7
Відповідь: 7см.
Малюнок В
- Знайдемо довжину сторони АС
Розглянемо трикутник АСВ - він прямокутний а значить АВ його гіпотенуза. Звідси за теоремой Піфагора (сумма квадратів катетів дорівнює квадрату гіпотенузи)
АС²+СВ²=АВ² → АС²=8²-6² → АС²=28 → АС=√28
- Знайдемо сторону АD або х
Розглянемо трикутник АDС - він прямокутний а значить АС його гіпотенуза. Звідси за теоремой Піфагора (сумма квадратів катетів дорівнює квадрату гіпотенузи)
AD²+CD²=AC² → AD²=(√28)²-(√21)² → AD²=7 → AD=√7
Відповідь: √7см.