Предмет: Алгебра,
автор: romaprihodko2006
Докажите тождество.
Интересно кто за это возьмётся)
Приложения:
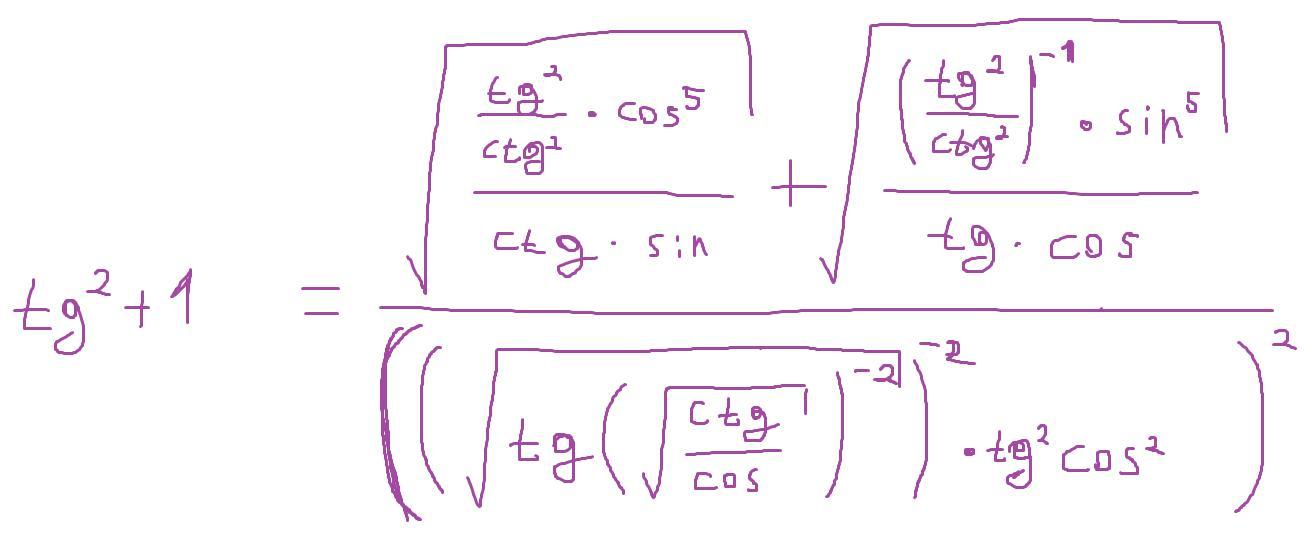
Universalka:
Я !
Ответы
Автор ответа:
2
Тождество доказано
Харош
Я просто похлопаю)
Не надо оваций :))
Можешь попробовать в моём профиле вторую задачку решить
Похожие вопросы
Предмет: Математика,
автор: 777777713
Предмет: Математика,
автор: Сергій1111
Предмет: Литература,
автор: Аноним
Предмет: Геометрия,
автор: Pavel1122opr
Предмет: Окружающий мир,
автор: Катеринка19516844