Question

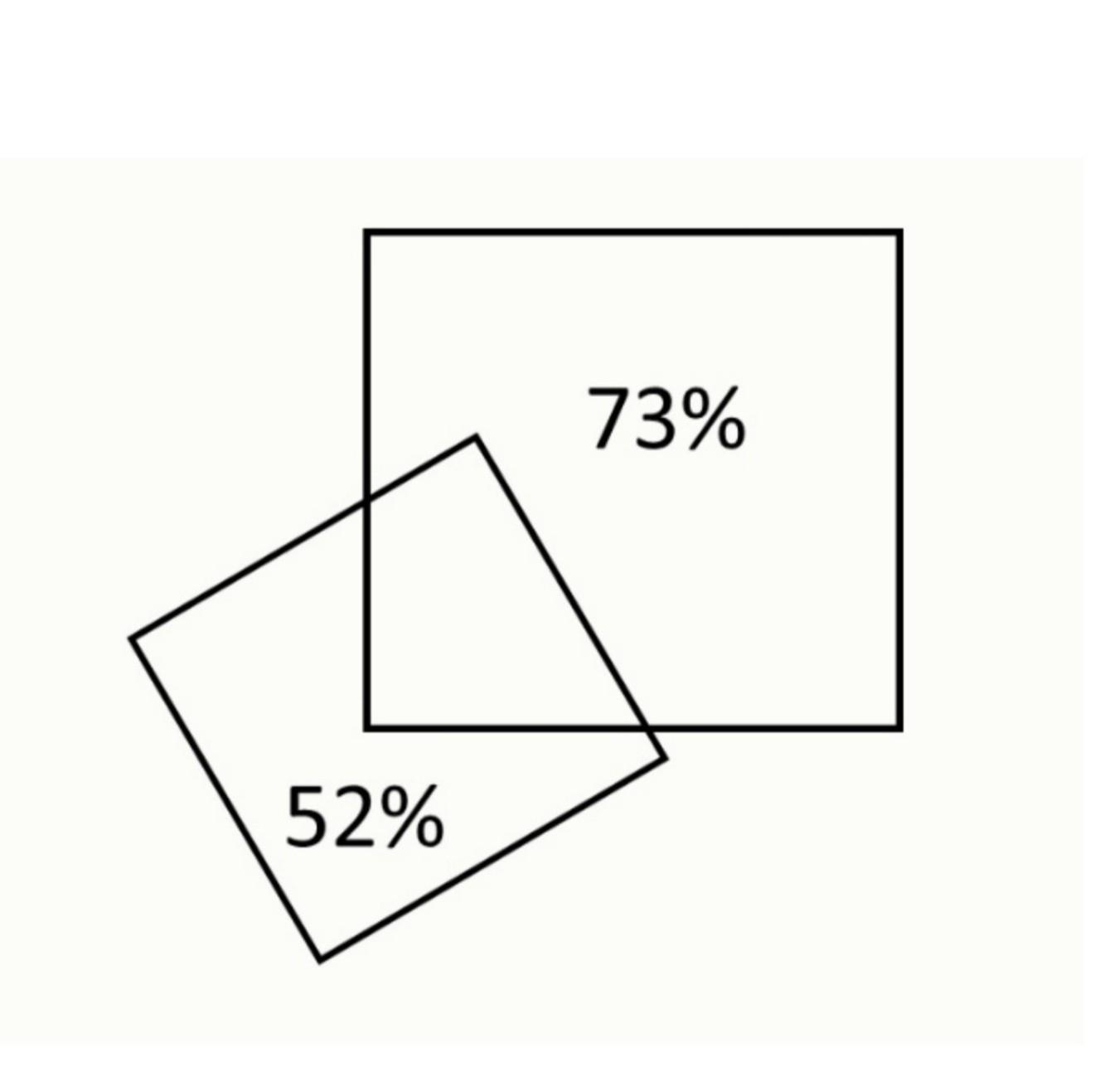
Два квадрата расположены так, как показано на рисунке. Если отсечь от маленького квадрата часть, пересекающуюся с большим, останется 52% его площади, у большого без их общей части останется 73% площади. Найдите, чему равно отношение стороны маленького квадрата к стороне большого.​

Answer 1

Ответ:

пусть а - сторона меньшего квадрата, А - сторона большего квадрата

площадь меньшего квадрата равна а^2, площадь большего А^2.

У квадратов есть некая общая часть, которая составляет 100%-52% = 48% от площади меньшего квадрата и 100%-73%=27% от площади большего.

0,48*а^2 = 0,27 * А^2

а^2/А^2 = 0,27/0,48

а^2/А^2 = 27/48 = 9/16

а/А= корень квадратный из 9/16 = 3/4

Ответ: а/А=3/4  

Answer 2

Ответ:3/4 или 0, 75

Пошаговое объяснение: Пусть а -сторона малого квадрата,

b -сторона большого квадрата.

 Тогда от маленького квадрата отрезали а²-0, 52а²=0,48а²

А их общая часть равна, той, что отсекли от большого квадрата:

b²-0,72b²= 0,28b²

⇒Cоставим уравнение: 0,48а²=0,28b²

48а²= 28b²

а²/b²=27/48=  9/16

(a/b)²= 9/16

a/b=3/4