Предмет: Геометрия,
автор: Polina250399
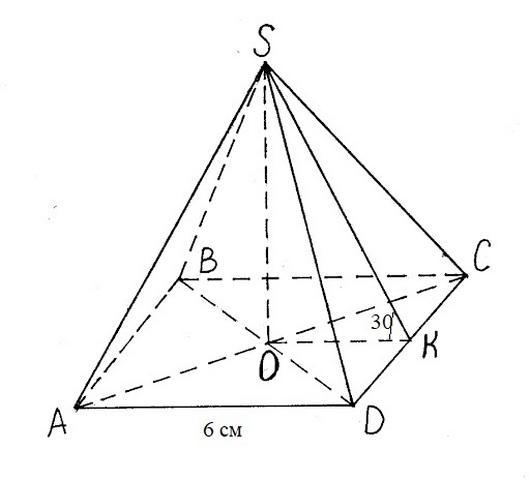
Сторона основания правильной четырехугольной пирамиды 6см. Двухгранные углы при основании равны 30°. Найдите площадь боковой поверхности пирамиды.
Полное решение и рисунок, пожалуйста
Ответы
Автор ответа:
1
Ответ:
Sбок=24√3 см²
Объяснение:
α=30°
a=6cм
Если у пирамиды углы при основании равны, то
Sбок=Sосн/cosα
Sосн=6*6=36 см²
Sбок=36/cos30°
Sбок=36:√3/2
Sбок=72/√3=24√3 см²
Или
Sбок=P/2*L, P- периметр, L-апофема
L=SK=OK/cosα(гипотенуза из ΔSOK)
OK=1/2a
L=a/(2*cosα)
Sбок=24*6/(2cos30°)
Sбок=24√3 см²
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: 253753
Предмет: Обществознание,
автор: mmm1721