Предмет: Математика,
автор: yapaco7137
Розв’яжіть диференціальні рівняння
Приложения:
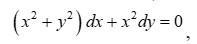
Ответы
Автор ответа:
3
Ответ:
линейное ДУ
Замена:
общее решение
hhehrhmhhhe:
можешь на мой вопрос ответит по математике
МНЕ ПОМОГИТЕ ПОЖАЛУЙСТА
Похожие вопросы
Предмет: Русский язык,
автор: 3903907
Предмет: Геометрия,
автор: Максимыч200226
Предмет: Қазақ тiлi,
автор: postol99
Предмет: Математика,
автор: сонечка281006
Предмет: Қазақ тiлi,
автор: нубик19