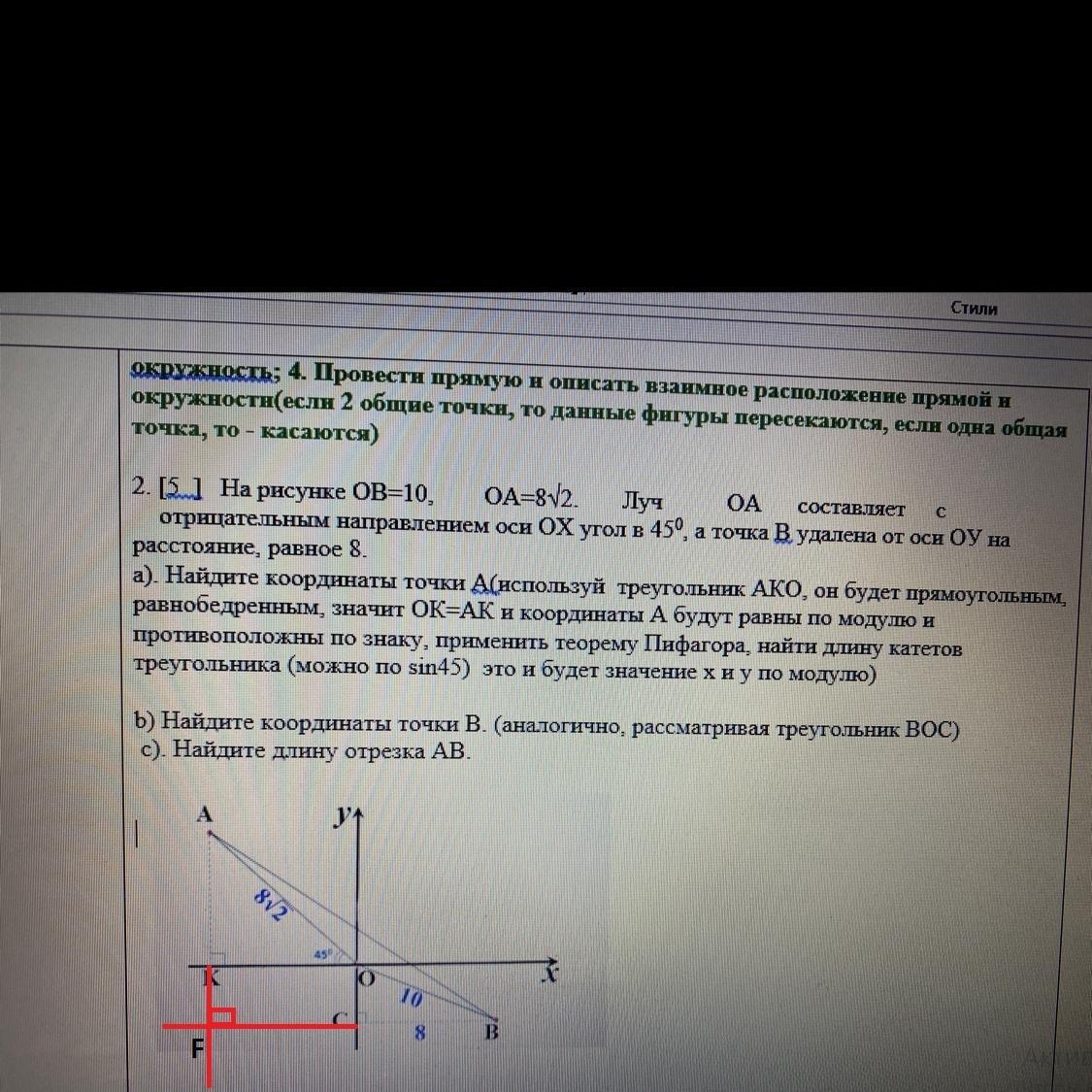
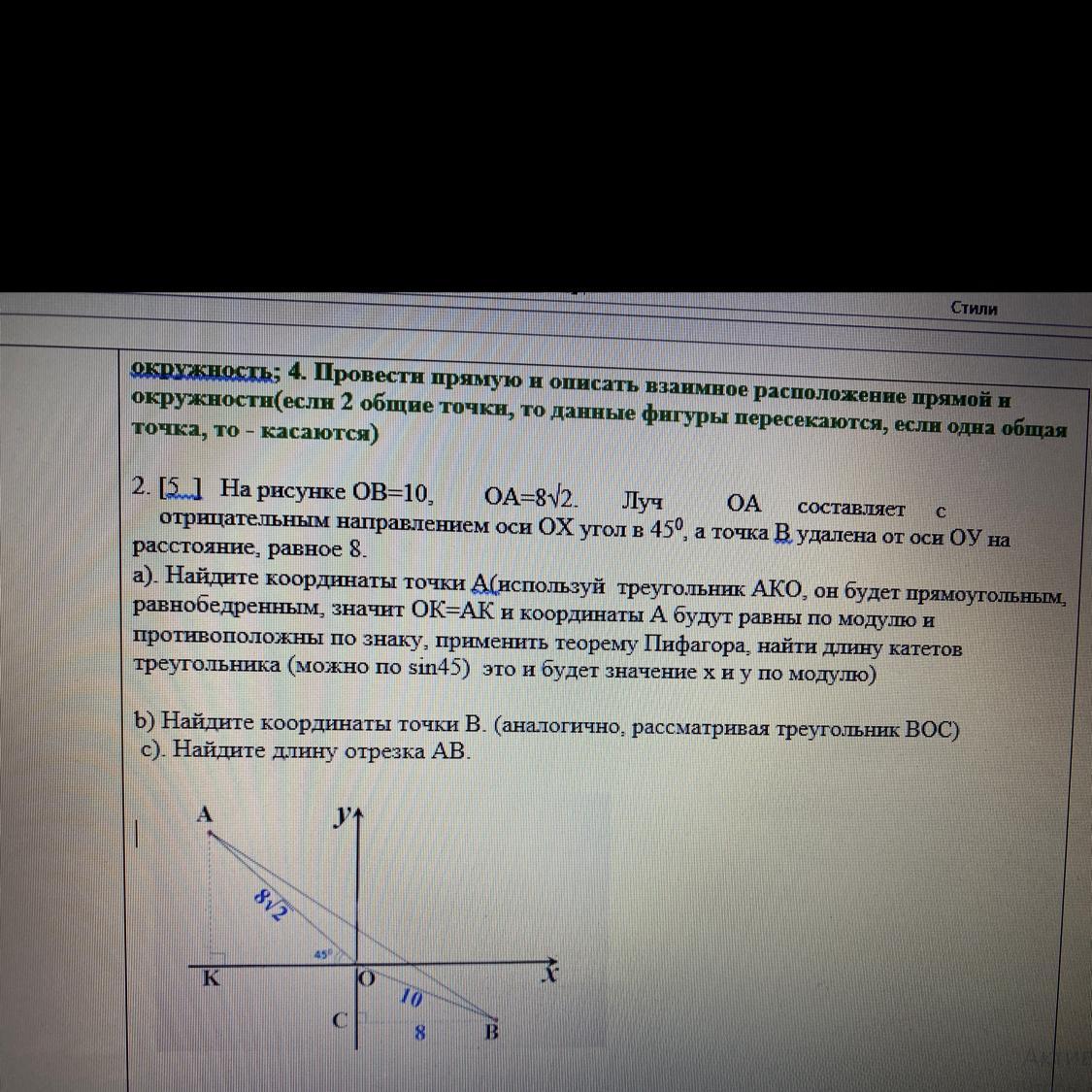
На рисунке ОВ=10, ОА=8√2. Луч ОА составляет с отрицательным направлением оси ОХ угол в 450, а точка В удалена от оси ОУ на расстояние, равное 8.
a). Найдите координаты точки А(используй треугольник АКО, он будет прямоугольным, равнобедренным, значит ОК=АК и координаты А будут равны по модулю и противоположны по знаку, применить теорему Пифагора, найти длину катетов треугольника (можно по sin45) это и будет значение х и у по модулю)
b) Найдите координаты точки В. (аналогично, рассматривая треугольник ВОС)
с). Найдите длину отрезка АВ.
Помогите пожалуйста СОЧ
Ответы
Ответ:
a) A(-8;8)
б) B(8;-6)
в)
Объяснение:
a)
Рассмотрим треугольник прямоугольный треугольник ΔKAO.
.
Так как треугольник ΔKAO - прямоугольный и один из его углов равен 45°, то по теореме данный треугольник равнобедренный, тогда AK = KO = 8. Отрезок KO - равен проекции отрезка AO на ось X. Отрезок AK -равен проекции отрезка AO на ось Y. Так как отрезки AK и KO находятся во второй координатной четверти, а точка O - начало координат, то координаты точки A(-8;8).
b)
Рассмотрим прямоугольный треугольник ΔBOC. По теореме Пифагора: .
Отрезок BC - проекция отрезка OB на ось X. Отрезок OC - равен проекции отрезка OB на ось Y. Так как отрезки OC и BC находятся в четвёртой координатной четверти, а точка O - начало координат, то координаты точки B(8;-6).
c)
Продлим отрезки AK и BC, пусть AK ∩ BC = F. Так как BC перпендикулярно оси ординат, а AK перпендикулярно оси абсцисс по условию, то угол ∠AFB = 90° и четырехугольник KOCF - прямоугольник. AF = AK + KF = AK + OC = 8 + 6 = 14.
BF = BC + CF = BC + KO = 8 + 8 = 16.Рассмотрим прямоугольный треугольник ΔAFB. По теореме Пифагора:
.