Question

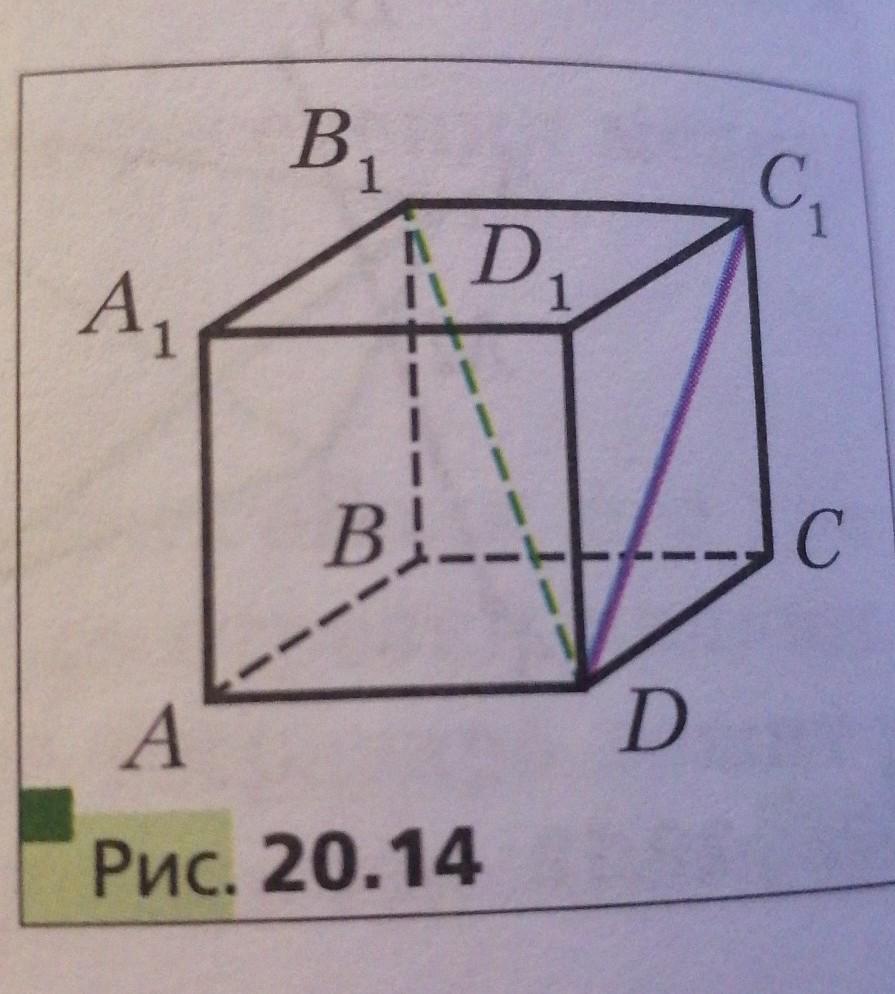
Дан прямоугольный параллепипед ABCDA1B1C1D1, AB=5 см, AD=7 см, AA1=12 см. Найдите угол между:
1) прямой DC1 и плоскостью A1B1C1;
2) прямой B1D и плоскостью ABC.
Фото чертежа ниже
Пожалуйста, дайте ответ в тетради или тут, но только на русском и чтобы было понятно​

Answer 1

Объяснение:

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

1) прямая DC1 и плоскость A1B1C1

DD1 ⊥ (A1B1C1) ⇒ DD1 ⊥ D1C1 ⇒ D1C1  - проекция прямой DC1 на плоскость A1B1C1, а ∠DС1D1 - искомый угол.

Рассмотрим ΔDС1D1 (∠D1=90°):  

D1C=A1B1=AB=5

DD1=AA1=12

tg ∠DС1D1 = D1D1/C1D1 = 12/5

∠DС1D1 = arctg (12/5)

2) прямая B1D и плоскость ABC

BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD ⇒ BD  - проекция прямой B1D на плоскость ABC, а ∠B1DB- искомый угол.

Рассмотрим ΔB1DB (∠B=90°):

BB1=AA1=12

BD найдём из прямоугольного ΔABD(∠A=90°) по т.Пифагора:

BD² =AB²+AD²=25+49=74

tg ∠B1DB=BB1/BD=  $\frac{12}{\sqrt{74} }$ =$\frac{12*\sqrt{74} }{\sqrt{74} *\sqrt{74} }$ = $\frac{6*\sqrt{74} }{37}$

∠B1DB= arctg $\frac{6*\sqrt{74} }{37}$