Question

Периметр прямоугольного треугольника, вписанного в круг, равен 27 см. Найдите периметр и площадь правого прямоугольника, нарисованного вне этого круга. Если не поняли вот другой тип этого же задание
Периметр правильного треугольника, вписанного в окружность, равен 27 см. Найдите периметр и площадь правильного четырехугольника, описанного около этой же окружности.

Answer 1

Ответ: 27 кв см

Условие задачи:

Периметр правильного треугольника, вписанного в окружность, равен 27 см. Найдите периметр и площадь правильного четырехугольника, описанного около этой же окружности.

Объяснение:

Найдем для начала, радиус вписанной окружности.

S=p*r, где  полупериметр р=27/2= 13,5 см, а радиус r - нужно найти.

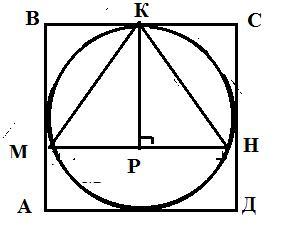
У правильного треугольника все стороны равны между собой  а углы равны 60° . Так что медиана, КР является и биссектрисой и высотой. Любая  сторона равна 27/3 = 9 см, следовательно из треугольника КРН

по определению косинуса

$cos(PKH) = cos 30 = \frac{KP}{KH}$

Отсюда  КР = КН* cos 30 = $9*\frac{\sqrt{3} }{2}$

Значит площадь треугольника равна

$S = 0,5*MH*KP = 0,5*9*9*\frac{\sqrt{3} }{2} = 81*\frac{\sqrt{3} }{4}$

Значит $r=\frac{S}{p} = 3\frac{\sqrt{3} }{2}$

Из рисунка очевидно, что сторона квадрата равна диаметру окружности, то есть

$a=2*r = 3\sqrt{3}$

Площадь квадрата равна

$S = a^2 =(3\sqrt{3})^2 = 27$ кв см