Предмет: Геометрия,
автор: meelfin
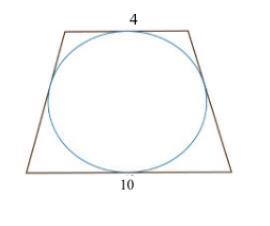
Найди площадь круга, вписанного в равнобедренную трапецию с основаниями длиной 4 см и 10 см.
Приложения:
Ответы
Автор ответа:
1
Ответ:
√10
Объяснение:
Формула радиуса вписанной окружности равнобочной трапеции (r):
r =
где
с - нижнее основание
b - верхнее основание
r = 1/2 * =
Похожие вопросы
Предмет: Физика,
автор: Владген
Предмет: Обществознание,
автор: ALFed
Предмет: Алгебра,
автор: Lilibang
Предмет: Математика,
автор: Еv04ka
Предмет: Химия,
автор: gorobets680831p76l7e