Предмет: Алгебра,
автор: Аноним
ПОМОГМТЕ ПОЖАЛУЙСТА СРОЧНООООООООООООООООООООО УМОЛЯЮЮ ВВААААСССССС
Приложения:
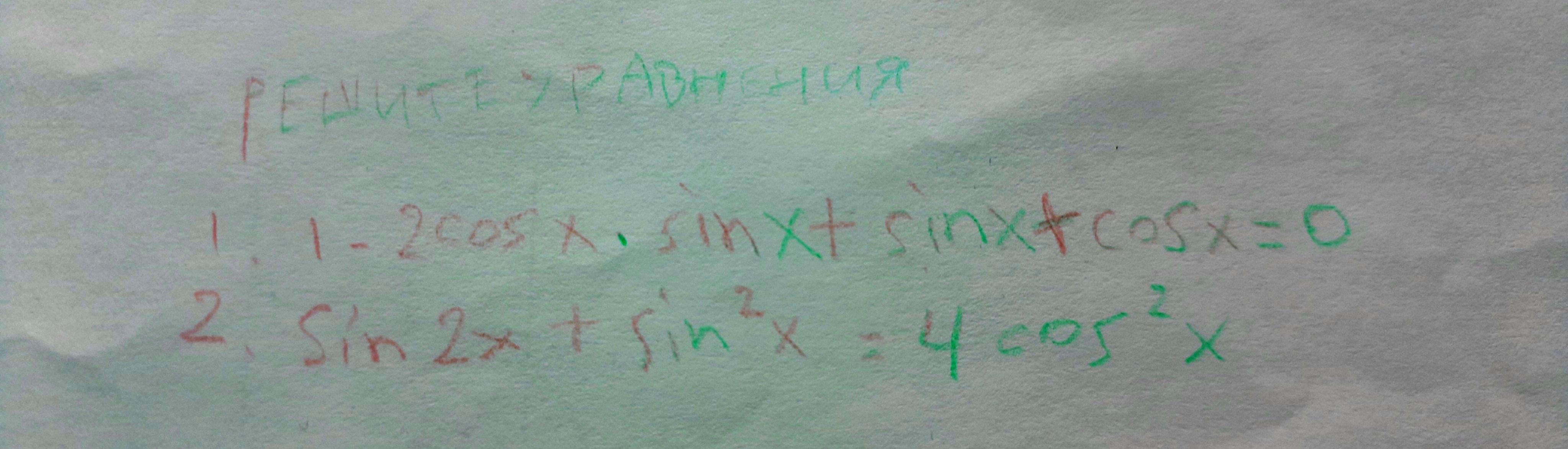
Аноним:
Нет последний не налоговой надо только первыыыыыыййййй
Не надооооо последний примеееееррр
ТОЛЬКО ПЕРВЫЙ ПОЖЖЖЖЖЖЖЖАЛУСТА
Ааааааа мне очень нужен первый примееееерр
Мне нужна оценка хорошояяяя
ПОСЛЕДНИЙ ПРИМЕР НЕ НУЖЕН
Я лопну как шар от нервов ,
На листочке если можно
1 пример
Ответы
Автор ответа:
1
Ответ:
Здравствуйте. А вот где буква u можно любую букву написать ?
да
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: 68928166
Предмет: Биология,
автор: Кристина210300
Предмет: Математика,
автор: esfaw