Предмет: Геометрия,
автор: bytyulka1939
У прямій трикутній призмі сторони основі дорівнюють
13 см, 14 см і 15 см. Через бічне ребро прізми і середню за
довжиною висоту основи проведено переріз, площа якого
60 см. Знайдіть об'єм призми.
Ответы
Автор ответа:
6
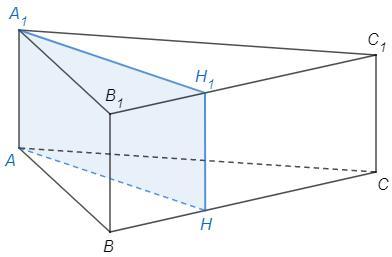
Рассмотрим основание ABC.
Наименьшая высота опушена к наибольшей стороне
наибольшая высота - к наименьшей стороне
средняя высота AH - к средней стороне BC=14
Следует из формулы площади треугольника:
Площадь ABC по формуле Герона
p =(13+14+15)/2 =21
S =√(21*8*7*6) =84
S =1/2 BC*AH => AH =2*84/14 =12
AA1H1H - данное сечение
(AH и ребра BB1 и CC1 скрещиваются, то есть не лежат в одной плоскости)
Боковые ребра прямой призмы перпендикулярны основанию (=> высота равна боковому ребру)
Сечение через боковое ребро прямой призмы - прямоугольник.
S(AA1H1H) =AA1*AH => AA1 =60/12 =5
V =S(ABC)*AA1 =84*5 =420 (см^3)
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: zhumabekovy2013
Предмет: Русский язык,
автор: annechka555
Предмет: Математика,
автор: angelok1515
Предмет: Математика,
автор: romans77
Предмет: Литература,
автор: 10201986m