Предмет: Алгебра,
автор: zhangir49
sinx I sin 3r+sin Sy-sm 74cos x cos 2rsin 4.x.
Приложения:
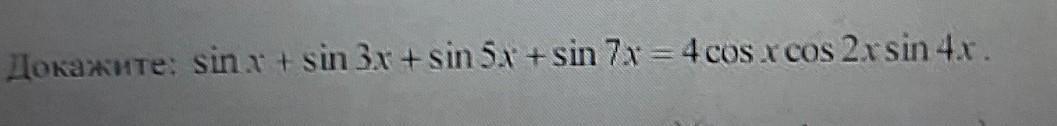
Ответы
Автор ответа:
1
Объяснение:
Проведем доказательство тождества следующим образом:
- проведем равносильные преобразования левой части доказываемого тождества;
- если в итоге преобразований левая часть примет ту же форму что и правая часть - тождество доказано.
Итак - левая часть:
Сгруппируем следующим образом:
Воспользуемся формулой суммы синусов:
Поочередно сложим группы внутри скобок:
Тогда вся левая часть примет вид:
для преобразования суммы косинусов в скобках воспользуемся такой формулой:
Выражение примет вид:
В результате преобразований левая часть приняла тот же вид что и правая.
Тождество доказано.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: dianaesmagan05
Предмет: История,
автор: egorshahmat
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: aikatyan1
Предмет: История,
автор: polialol