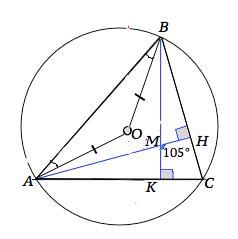
Около остроугольного треугольника АВС описана окруженость с центром О. Высоты АН и ВК треугольника пересекаются в точке М, = 105° . Найдите угол ABO.
Ответы
Треугольник остроугольный => высоты пересекаются внутри треугольника.
Пусть угол BAK равен alfa, тогда из прямоугольного треугольника ABK: угол ABK = 90 - alfa
Пусть угол ABC равен beta, тогда из прямоугольного треугольника ABH: угол HAB = 90 - beta
Из рассмотрения треугольника ABM: сумма углов равна 180 градусов;
AMB + MAB + MBA = 180
105 + (90-alfa) + (90-beta) = 180
Отсюда alfa + beta = 105 (град)
Сумма углов треугольника ABC равна 180 градусов, тогда
угол ACB = 180 - (ABC+BAC) = 180 - (alfa+beta) = 180 - 105 = 75 (град)
Тогда угол AOB = 2 * ACB = 150 град (O — центр окружности; A, B, C лежат на ней)
Далее, треугольник ABO — равнобедренный (AO и BO — радиусы одной окружности) , поэтому углы при основании равны:
OAB = ABO = (1/2) * (180 - AOB) = (180-150)/2 = 15 (градусов) .
ОТВЕТ: угол ABO = 15 градусов.
Ответ: 15°
Вариант решения:
В четырехугольнике КМНС ∠К=∠Н=90° ( АН и ВК – высоты). Сумма углов четырехугольника 360°.⇒ ∠С=360°-2•90°-105°=75°.
Угол АСВ – вписанный, поэтому градусная мера дуги АВ, на которую он опирается, вдвое больше. ◡АВ=2•75°=150°
Градусная мера центрального угла АОВ равна мере дуги АВ. ∠АОВ=150°.
Треугольник АОВ равнобедренный ( ОА=ОВ – радиусы). ⇒
Из суммы углов треугольника ∠АВО=∠ВАО=(180°-150°):2=15°.