Предмет: Геометрия,
автор: nastlatrenbah10
Условие задания:
Один из острых углов прямоугольного треугольника равен 60°, а сумма меньшего катета и гипотенузы
равна 45 см.
Определи длину меньшего катета.
1. Величина второго острого угла равна
2. Длина меньшего катета равна
см.
Ответы
Автор ответа:
2
Ответ:
1. Второй острый угол равен 30, так как 180 - (90 + 60) = 30
2. По теореме сторона противоположная углу 30 градусов, равна половине гипотенузы.
Объяснение:
Приложения:
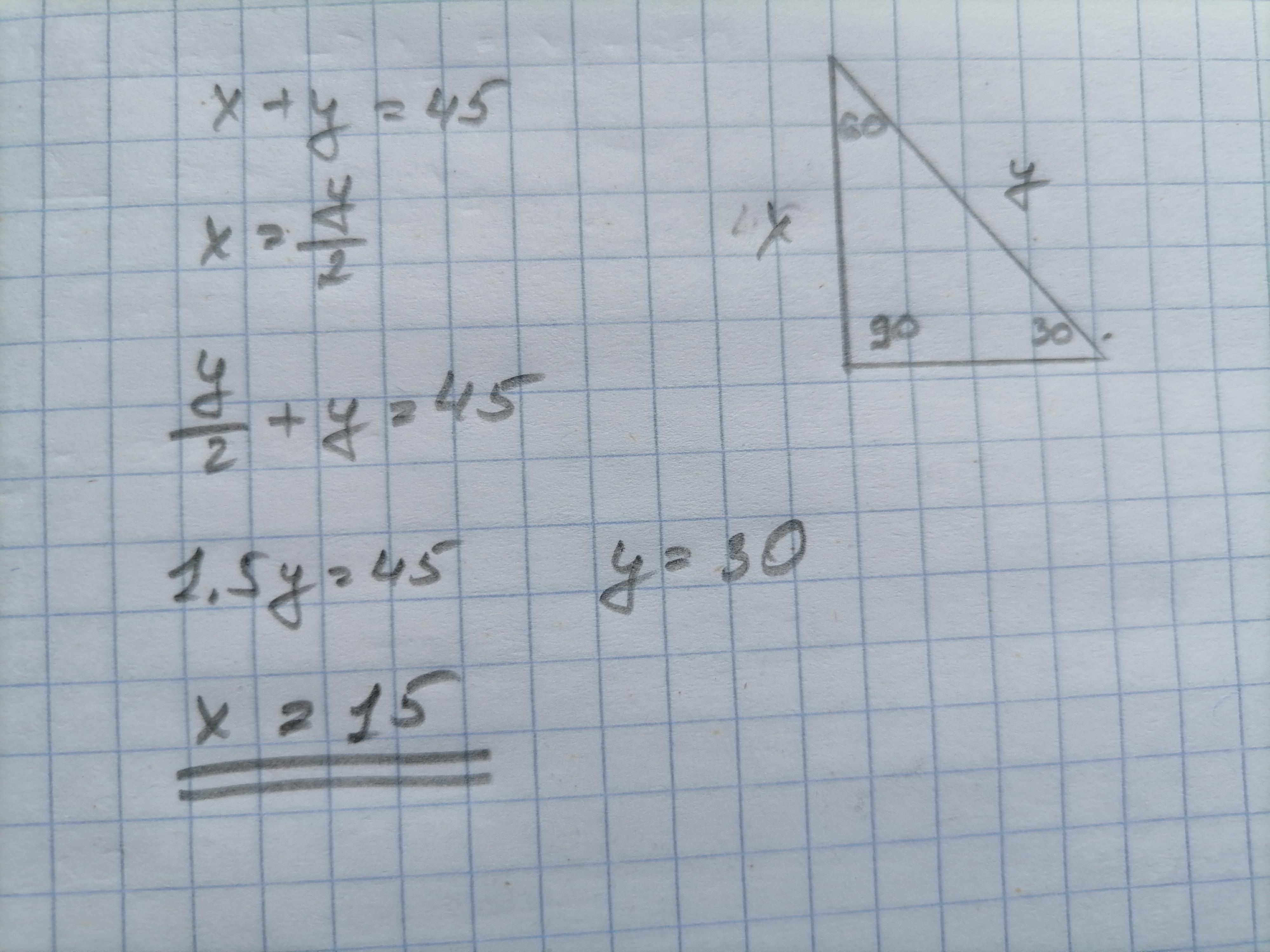
Автор ответа:
2
Ответ:
Удачи)
Объяснение:
/_ - кут
Сумма гострих кутов прямоугольного треугольника 90°
/_1=60°,/_2=90-60=30°
Напроти больше сторони лежит большой угол, напроти меньшей сторони менший угол, следовательно короткий катет лежит проти угла 30°
Катет лежащий проти угла 30°,равен половинок гипотенузи
Пусть короткий катет=х см, следовательно гипотенузи=2х см
По условию Сумма котрого котроткого катета и гипотенузы 45 см составим уравение :
2х+х=45
3х=45
х=45:3
х=15(см)меньший катет
Похожие вопросы
Предмет: Математика,
автор: nargizz2015
Предмет: Химия,
автор: VG9790
Предмет: Немецкий язык,
автор: SkaiFall1
Предмет: История,
автор: Xex111
Предмет: Алгебра,
автор: di52248