привидите 3 примера диапазонов,
Перечислите функции работы с диапазонами и их назначение
Опишите принцип относительности и его следствие ПЖ помогите
Ответы
Во первых, диапазон представляет собой набор из двух и более ячеек.
1-ый пример: Диапазон B2։C4 — можно выделить, кликнув по нижнему правому углу ячейки В2 и протянув указатель мыши до ячейки C4.
2-ой пример: Можно выделить диапазон, который состоит из отдельных несмежных ячеек, зажав клавишу Ctrl и кликнув по каждой ячейке, которую надо включить в диапазон.
3-ой пример: Выделим большой диапазон ячеек: клавиша F5 или Ctrl+G. В появившемся окне, в поле «Ссылка» введё, адрес: B3:D12345 (или b3:d12345) и нажмём ОК.
Вычисления в таблицах программы Excel осуществляются при помощи формул. Формула состоит из:
1.знаки арифметич. операций;
2.сonst числовые или текстовые;
3.название встроенных функций;
4.разделители;
5.ссылки.
Формула — может содержать ссылки, то есть адреса ячеек, содержимое которых используется в вычислениях.
Что и означает, что результат вычисления формулы зависит от числа, находящегося в другой ячейке.
Ячейка,содержащая формулу,таким образом,является зависимой. Значение,отображаемое в ячейке с формулой — пересчитывается при изменении значения ячейки,на которую указывает ссылка.
Ссылки:
1.абсолютные;
2.относительные;
3.смешанные.
Примеры работы функции области:
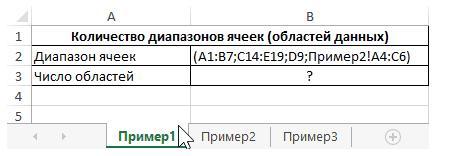
1. Надо Вернуть число, соответствующее количеству областей в диапазонах A1:B7, C14:E19, D9, Пример2!A4:C6.
Исходные данные на листе «Пример1» (смотри первую картинку).
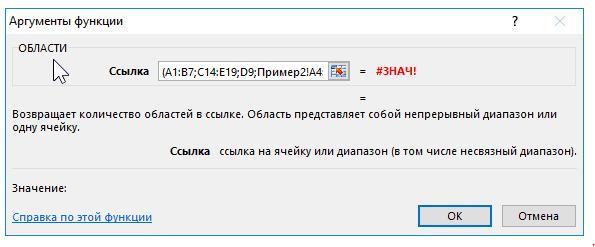
Для подсчета количества областей используем формулу: (вторая каритнка)
Результат вычисления функции является ошибка #ЗНАЧ!, поскольку диапазон «Пример2!A4:C6» находится на другом листе.
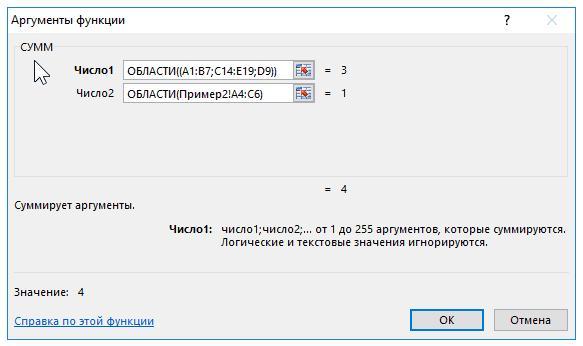
Для решения задачи используем формулу с помощью функции СУММ (третья картинка):
Данная функция — вычисляет сумму полученных значений в результате выполнения функций ОБЛАСТИ для подсчета количества областей в диапазонах A1:B7;C14:E19;D9 и Пример2!A4:C6 соответственно.
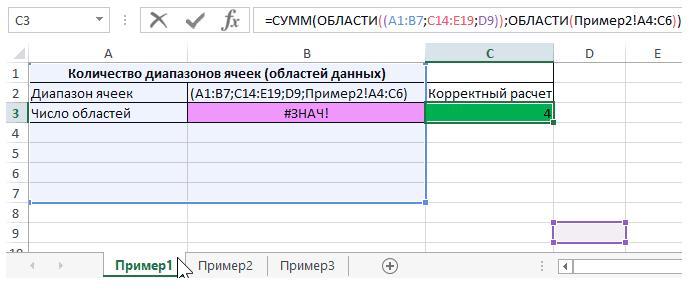
Результат таков (четвёртая картинка):
Принципа относительности:
Это фундаментальный физический принцип, один из принципов симметрии, согласно чему — все физические процессы в инерциальных системах отсчёта — протекают одинаково. Это также не завсит от того, неподвижна ли система или находится ли она в состоянии равномерного и прямолинейного движения.
Следствие: все законы природы одинаковы во всех инерциальных системах отсчёта.
Один из примеров может быть поезд, двигающийся по рельсам, или планета, которая вращающается вокруг Солнца.