Предмет: Математика,
автор: Vika7love
Помогите пожалуйста. Найдите интеграл :
Приложения:
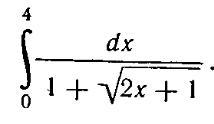
Ответы
Автор ответа:
0
Ответ:
Замена:
Похожие вопросы
Предмет: Биология,
автор: Юсуфовна
Предмет: Алгебра,
автор: MrLend
Предмет: Литература,
автор: nataxa861
Предмет: Математика,
автор: MishkaDmitriev
Предмет: Русский язык,
автор: lovenew