Предмет: Алгебра,
автор: chelyshev05
Помогите решить!! Три примера по логарифмам
Приложения:
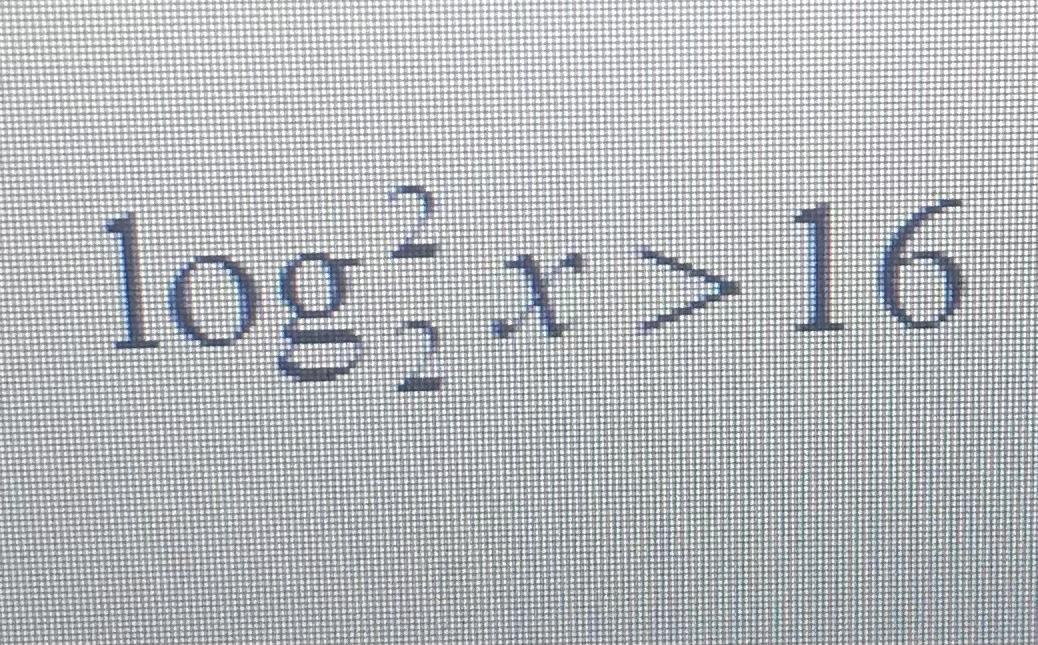
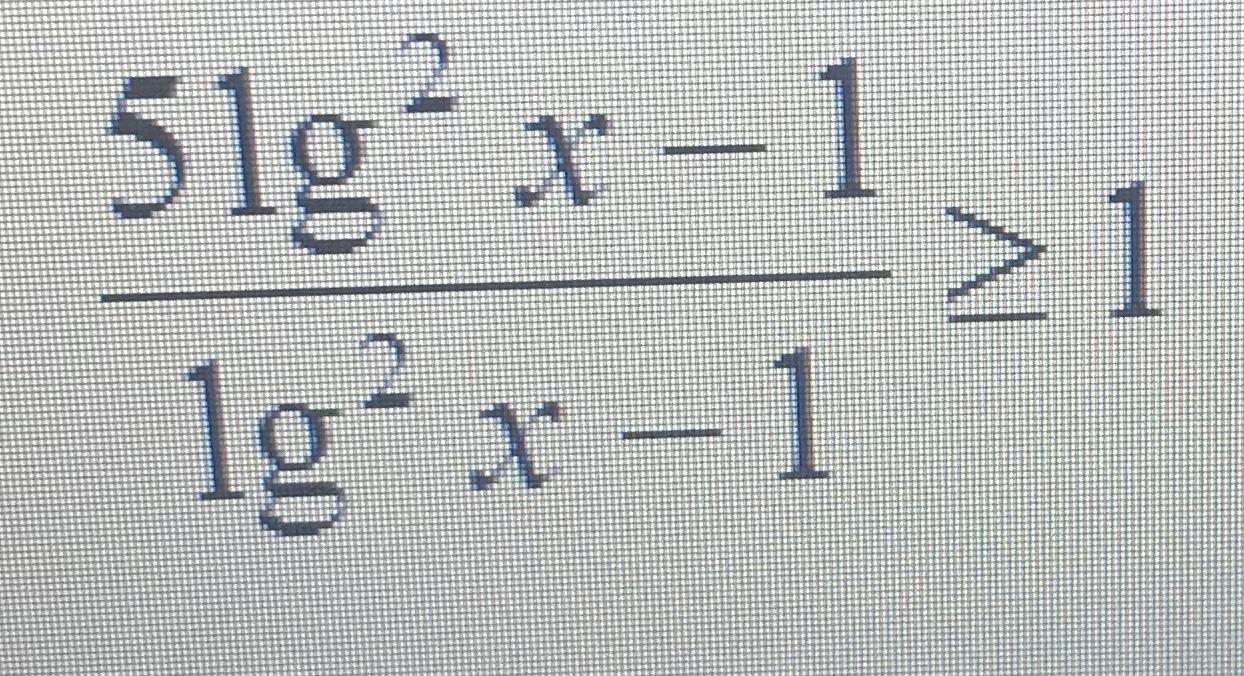
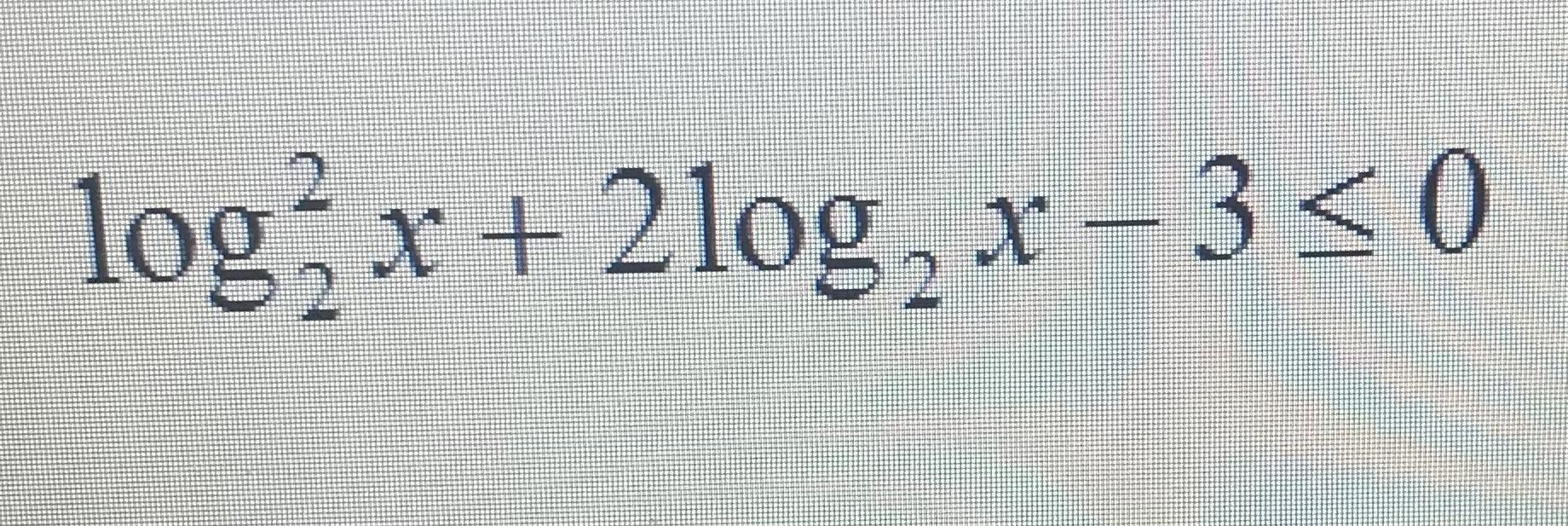
Ответы
Автор ответа:
2
1.
С ОДЗ:
2.
Пусть lgx = t
Ответ вместе с ОДЗ:
х ∈ (0; 0,1)U{1}U(10; + беск)
3.
Пусть
- ответ
Автор ответа:
3
Ответы с решениями во вложении
Объяснение: там же
Приложения:

Похожие вопросы
Предмет: Математика,
автор: iiskraa
Предмет: Литература,
автор: Buttowski89
Предмет: Математика,
автор: ZZZZZSWISSZZZZZ
Предмет: Биология,
автор: fkvadim
Предмет: Физика,
автор: цветок93