Предмет: Геометрия,
автор: myjenyamail
Решите задачу :
Через точку C окружности с центром О проведена касательная к этой окружности, АВ - диаметр окружности. Из точки А на косательную отпущен пепенддикцляр АD. Докажите, что луч АС - биссектриса угла BAD. Рисунок который я нарисовала по условию прикреплён.
Приложения:
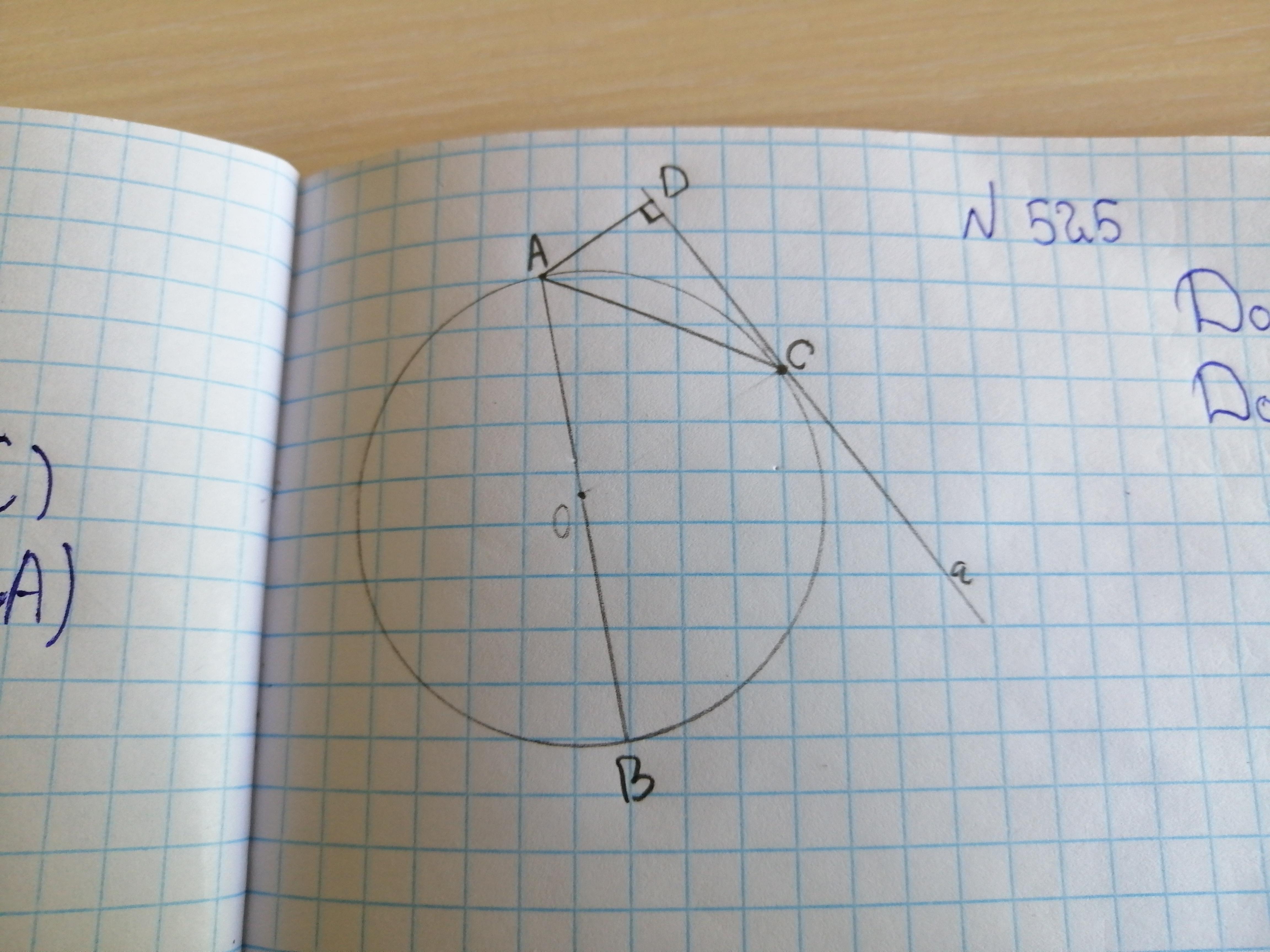
Ответы
Автор ответа:
0
Ответ:
ДАНО: окружность, AB-диаметр, DM-касательная, DA перпенд. DM
Док-ть: АС- биссектриса угла BAD
ДОКАЗАТЕЛЬСТВО: проведем диаметр AB, такой, что он параллелен DM;
проведем перпендикуляр из центра окружности к касательной;
также проведем луч AC.
Рассмотрим прямоугольник ADCO: AO=OC(как радиусы), СO= DA(т.к. прямые DM и AB параллельны, а OC и DA - перпендикуляры)
Рассмотрим треугольник АСО: угол О=90 градусов, АО=ОС => треугольник равнобедренный => угол САО=АСО= (180-90)\2= 45 градусов
Угол АСО = DAC(как накрест лежащие при параллельных прямых АВ и DM)
И так как угол DAO равен углу САО(DAO=CAO=45),то АС является биссектрисой угла OAD(или BAD- это просто один и тот же угол)
Объяснение:
myjenyamail:
Спасибо, но ведь в условии не сказано, что АВ паралельна DM
Такое может быть, но так как это не сказано в условии мы не можем это использовать
Похожие вопросы
Предмет: География,
автор: KristinaKey
Предмет: Английский язык,
автор: Мосрентген
Предмет: Физика,
автор: angelina20091
Предмет: Алгебра,
автор: Аноним
Предмет: Литература,
автор: Skammyerus